|
|
giải đáp
|
véctơ
|
|
|
|
d) $\overrightarrow{AB}=\overrightarrow{DC}$
$\overrightarrow{AD}=\overrightarrow{BC}$
|
|
|
|
sửa đổi
|
véctơ
|
|
|
|
c) Các vecto ngược hướng$\overrightarrow{AB}$ và $\overrightarrow{BA}$ $\overrightarrow{AD}$ và $ \overrightarrow{CB}$ $\overrightarrow{IA}$ và $ \overrightarrow{IC}$ $\overrightarrow{IB}$ và $ \overrightarrow{ID}$
c) Các vecto ngược hướng$\overrightarrow{AB}$ và $\overrightarrow{CD}$ $\overrightarrow{AD}$ và $ \overrightarrow{CB}$ $\overrightarrow{IA}$ và $ \overrightarrow{IC}$ $\overrightarrow{IB}$ và $ \overrightarrow{ID}$
|
|
|
|
giải đáp
|
véctơ
|
|
|
|
c) Các vecto ngược hướng
$\overrightarrow{AB}$ và $\overrightarrow{CD}$
$\overrightarrow{AD}$ và $ \overrightarrow{CB}$
$\overrightarrow{IA}$ và $ \overrightarrow{IC}$
$\overrightarrow{IB}$ và $ \overrightarrow{ID}$
|
|
|
|
giải đáp
|
véctơ
|
|
|
|
b) Các vecto cùng hướng
$\overrightarrow{AB}$ và $ \overrightarrow{DC}$
$\overrightarrow{AC}$ và $ \overrightarrow{AI}$
$\overrightarrow{AD}$ và $ \overrightarrow{BC}$
$\overrightarrow{BD}$ và $ \overrightarrow{BI}$
|
|
|
|
giải đáp
|
véctơ
|
|
|
|
a) Các vecto cùng phương
$\overrightarrow{AB}$ và $ \overrightarrow{DC}$
$\overrightarrow{AD}$ và $ \overrightarrow{BC}$
$\overrightarrow{AI}$ và $ \overrightarrow{AC}$
$\overrightarrow{BI}$ và $ \overrightarrow{BD}$
|
|
|
|
sửa đổi
|
Bất đẳng thức nhé
|
|
|
|
a) $(1+\frac{1}{1.3})(1+\frac{1}{2.4})...(1+\frac{1}{n(n+2)})<2 $ Chú ý $1+\frac{1}{n(n+2)}=\frac{(n+1)^2}{n(n+2)}$. Do đó $(1+\frac{1}{1.3})(1+\frac{1}{2.4})...(1+\frac{1}{n(n+2)})=\frac{2^2}{1.3}.\frac{3^2}{2.4}\cdots\frac{(n+1)^2}{n(n+2)}=\frac{2.(n+1)!^2}{n!.(n+2)!}=\frac{2}{n+2}<2 $
a) $(1+\frac{1}{1.3})(1+\frac{1}{2.4})...(1+\frac{1}{n(n+2)})<2 $ Chú ý $1+\frac{1}{n(n+2)}=\frac{(n+1)^2}{n(n+2)}$. Do đó $(1+\frac{1}{1.3})(1+\frac{1}{2.4})...(1+\frac{1}{n(n+2)})=\frac{2^2}{1.3}.\frac{3^2}{2.4}\cdots\frac{(n+1)^2}{n(n+2)}=\frac{2.(n+1)!^2}{n!.(n+2)!}=\frac{2(n+1)}{n+2}<2 $
|
|
|
|
sửa đổi
|
Một bạn trên facebook hoi bài này,mình đăng giúp
|
|
|
|
Gọi $SO$ là đường cao của hình chóp thì $SO \perp (ABC)$ và $O \in mp(ABC).$Do các cạnh bên tạo với đáy góc $45^\circ$ nên từ định nghĩa góc tạo bởi đường thẳng và mặt phẳng suy ra$\widehat{SAO}=\widehat{SBO}=\widehat{SCO}=45^\circ$Do đó $SAO, SBO, SCO$ là các tam giác vuông cân nên $AO=BO=CO$ vì đều bằng $SO.$Từ đây suy ra $O$ là tâm đường tròn ngoại tiếp của tam giác vuông $ABC$ tại $C$ nên nó là trung điểm $BC$Kéo theo $SO=AO=\frac{1}{2}BC$Mặt khác tam giác vuông $ABC$ tại $C$ có $A=60^\circ$ nên $BC=\frac{AC}{\cos 60}=2a$Theo định lý Pytago ta tính được $BC=\sqrt{AB^2-AC^2}=\sqrt{(2a)^2-a^2}=a\sqrt 3$Vậy $V_{S.ABC}=\frac{1}{3}SO.S_{ABC}=\frac{1}{3}.\frac{1}{2}BC.\frac{1}{2}BC.AC=\frac{a^3\sqrt 3}{3}$ (đơn vị diện tích).
Gọi $SO$ là đường cao của hình chóp thì $SO \perp (ABC)$ và $O \in mp(ABC).$Do các cạnh bên tạo với đáy góc $45^\circ$ nên từ định nghĩa góc tạo bởi đường thẳng và mặt phẳng suy ra$\widehat{SAO}=\widehat{SBO}=\widehat{SCO}=45^\circ$Do đó $SAO, SBO, SCO$ là các tam giác vuông cân nên $AO=BO=CO$ vì đều bằng $SO.$Từ đây suy ra $O$ là tâm đường tròn ngoại tiếp của tam giác vuông $ABC$ tại $C$ nên nó là trung điểm $BC$Kéo theo $SO=AO=\frac{1}{2}BC$Mặt khác tam giác vuông $ABC$ tại $C$ có $A=60^\circ$ nên $BC=\frac{AC}{\cos 60}=2a$Theo định lý Pytago ta tính được $BC=\sqrt{AB^2-AC^2}=\sqrt{(2a)^2-a^2}=a\sqrt 3$Vậy $V_{S.ABC}=\frac{1}{3}SO.S_{ABC}=\frac{1}{3}.\frac{1}{2}BC.\frac{1}{2}BC.AC=\frac{a^3\sqrt 3}{3}$ (đơn vị diện tích).
|
|
|
|
giải đáp
|
Một bạn trên facebook hoi bài này,mình đăng giúp
|
|
|
|
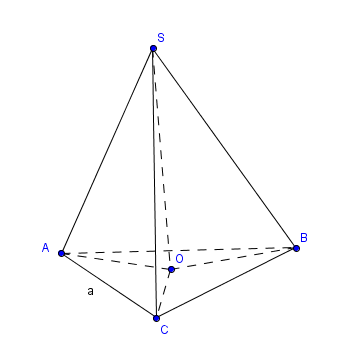 Gọi $SO$ là đường cao của hình chóp thì $SO \perp (ABC)$ và $O \in mp(ABC).$ Do các cạnh bên tạo với đáy góc $45^\circ$ nên từ định nghĩa góc tạo bởi đường thẳng và mặt phẳng suy ra $\widehat{SAO}=\widehat{SBO}=\widehat{SCO}=45^\circ$ Do đó $SAO, SBO, SCO$ là các tam giác vuông cân nên $AO=BO=CO$ vì đều bằng $SO.$ Từ đây suy ra $O$ là tâm đường tròn ngoại tiếp của tam giác vuông $ABC$ tại $C$ nên nó là trung điểm $BC$ Kéo theo $SO=AO=\frac{1}{2}BC$ Mặt khác tam giác vuông $ABC$ tại $C$ có $A=60^\circ$ nên $BC=\frac{AC}{\cos 60}=2a$ Theo định lý Pytago ta tính được $BC=\sqrt{AB^2-AC^2}=\sqrt{(2a)^2-a^2}=a\sqrt 3$ Vậy $V_{S.ABC}=\frac{1}{3}SO.S_{ABC}=\frac{1}{3}.\frac{1}{2}BC.\frac{1}{2}BC.AC=\frac{a^3\sqrt 3}{3}$ (đơn vị diện tích). |
|
|
|
|
|
giải đáp
|
Cho em nốt 1 bài nhé,hỏi nhiều sợ các bạn uýnh lém
|
|
|
|
b) Nếu ở đề bài không có điều kiện $x, y>0$ thì ta phải dùng phương pháp hàm số.
$B=f(x)=x(1-x)^3\Rightarrow f'(x)=(x-1)^2(1-4x)$
Lập bảng biến thiên của hàm số này và ta được
$\max B = \max f(x)=\frac{27}{256}\Leftrightarrow \begin{cases}x=1/4 \\ y=3/4 \end{cases}$
|
|
|
|
bình luận
|
Thêm bài này các ad ơi
Hãy ấn chữ V dưới đáp án để chấp nhận nếu như bạn thấy lời giải này chính xác, và nút mũi tên màu xanh để vote up nhé. Thanks!
|
|
|
|
|
|
|
|
giải đáp
|
Thêm bài này các ad ơi
|
|
|
|
c) Hiển nhiên thấy
$\frac{1}{ \sqrt{1}+ \sqrt{2}}+ \frac{1}{ \sqrt{2}+ \sqrt{3}}+...+\frac{1}{ \sqrt{11}+ \sqrt{12}}=\left ( \sqrt{2}- \sqrt{1} \right )+\left ( \sqrt{3}- \sqrt{2} \right )+...+\left ( \sqrt{12}- \sqrt{11} \right )= \sqrt{11}- 1 $
Mà $2< \sqrt{11}- 1 <3$ nên có đpcm.
|
|
|
|
bình luận
|
Thêm bài này các ad ơi
Hãy ấn chữ V dưới đáp án để chấp nhận nếu như bạn thấy lời giải này chính xác, và nút mũi tên màu xanh để vote up nhé. Thanks!
|
|
|
|
|
|
|
|
|
|