a/ Chú ý: câu a là câu gợi ý cho ta cách vẽ hình!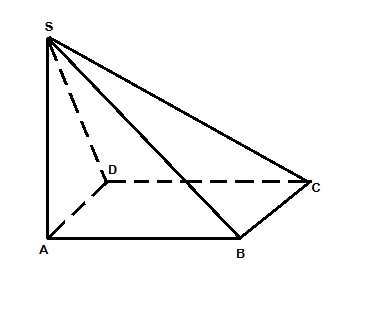

Có: CD vuông góc với  SD, CD vuông góc với  DA => CD vuông góc với  (SAD) => CD vuông góc với  SA (1)
 CB vuông góc với  SB, CB vuông góc với  BA => CB vuông góc với  (SAB) => CB vuông góc với  SA (2)
(1)(2)=> SA vuông góc với mp(ABCD)

+ Tính SA
 Có: $SC^{2}=SD^{2}+DC^{2}$ => $SC^{2}=6a^{2}$
$AC^{2}=AB^{2}+BC^{2}$  => $AC^{2}=4a^{2}$
Mà  $SC^{2}=SA^{2}+AC^{2}$ => $SA^{2}=2a^{2}$ => SA= a$\sqrt{2}$

Lời giải này có yêu cầu trả vỏ sò để xem. Bạn hãy link trên để vào xem chi tiết

2/ Vì EMNF là hình thang vuông nên:
$S_{EMNF}$= 1/2. (EM+EN). EF (1)

+Có EM là đường trung bình trong tam giác SAB => EM= 1/2AB= a (2)
 
+ Tính FN: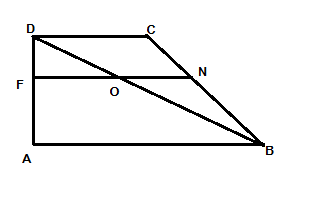

Có: $\frac{FO}{AB}=\frac{DF}{DA}=\frac{x}{a}$ => FO= 2x

Có: $\frac{ON}{DC}=\frac{BN}{BC}=\frac{AF}{AD}=\frac{a-x}{a}$ => ON= a-x
=> FN= a+x (3)

+ Có: $EF^{2}=EA^{2}+AF^{2}=a^{2}+x^{2}$ => EF= $\sqrt{a^{2}+x^{2}}$ (4)
(1)(2)(3)(4) => $S_{EMNF}$= 1/2. (2a+x). $\sqrt{a^{2}+x^{2}}$
 

Cho A là ma trận vuông cấp n có dạng:
A= ($a_{ij}$) , $a_{ij}$= i+j, i,j= 1,2,.........,n
Tính hạng của ma trận A? 

Cho ma trận
A= $\begin{pmatrix}2 & -1&0&0\\ 0 & 2&-1&0\\ 0&0&2&-1\\ 0&0&0&2\end{pmatrix}$
Tìm tất cả các ma trận thực vuông X cấp 4 sao cho AX= XA 

Gỉa sử: x,y>0 thỏa mãn: $a.x^{2}+b.y^{2}=c$ (a,b,c>0)
Tìm Min M= $d.x^{n}+e.y^{n}$
a,b,c,d,e tùy chọn 

Lời giải này có yêu cầu trả vỏ sò để xem. Bạn hãy link trên để vào xem chi tiết

Gắn hình vẽ vào trong hệ trục tọa độ sao cho D trùng với gốc tọa độ, DA trùng Ox, DC trùng Oy, DS trùng Oz
Khi đó tọa độ các điểm như sau: D(0,0,0); A(a,0,0), B(a,a,0), C(0,2a,0),S(0,0,a)
Gọi I là tâm mặt cầu ngoại tiếp tứ diện ASBC
Khi đó $\overrightarrow{AI}$ (x-a,y,z)
 $\overrightarrow{BI}$ (x-a,y-a,z)
$\overrightarrow{CI}$ (x,y-2a,z)
$\overrightarrow{SI}$ (x,y,z-a) 
Có AI=BI => $y^{2}=(y-a)^{2}$ 
AI=CI => $(x-a)^{2}+y^{2}= x^{2}+(y-2a)^{2}$ 
AI=SI => $(x-a)^{2}+z^{2}= x^{2}+(z-a)^{2}$  
=> x= -3a/8; y=a/2; z=-3a/8
=> AI= $\sqrt{\frac{146a^{2}}{64}}$ 

+/ Theo chứng minh trên, BC vuông góc với (SAB) => BC vuông góc với AH
Mà AH vuông góc với SB
=> AH vuông góc với (SBC)
=> AH vuông góc với SC 

+/ $\Delta$SAC vuông tại A => SA vuông góc với AC, mà SA vuông góc với AB => SA vuông góc với (ABC) => BC vuông góc vứoi SA
Mà BC vuông góc vứoi AB
=> BC vuông góc với (SAB) => BC vuông góc với SB => $\Delta$SBC vuông tại B 

3/ Mình sửa lại đề bài như sau, bạn xem lại xem có đúng không nhé Chứng minh: AD' vuông góc với CB' chứ không phải là CD' (chắc bạn nhầm thôi)
Có DCB'A' là hình chữ nhật => CB' //DA', mà AD' vuông góc với DA'
=> AD' vuông góc với CB' 

2/ Có BC song song và bằng A'D' => BCD'A' là hình bình hành => CD'//BA'
Mà AB' vuông góc với BA'
=> AB' vuông góc với CD' 

1/ B'D' vuông góc với A'C', B'D' vuông góc với AA' => B'D' vuông góc với (ACC'A') => B'D' vuông góc với AC

a/ BD vuông góc với AC, BD vuông góc với AA' => BD vuông góc với (ACC'A')
=> BD vuông góc ới AC' 

b/ Gắn hệ trục tọa độ vào hình vẽ sao cho A' trùng với gốc tọa độ, A'B' trùng Ox, A'D' trùng Oy, A'A trùng Oz
Khi đó, tọa độ các điểm là: A' (0,0,0), C(a,a,a), N(a,0,a/2), M(0,a/2,a)
=> $\overrightarrow{A'C}$(a,a,a); $\overrightarrow{MN}$(a,-a/2,-a/2)
=>  $\overrightarrow{A'C}$. $\overrightarrow{MN}$=$\overrightarrow{0}$
=> A'C vuông góc với MN