a/ 4 bộ phận có diện tích bằng nhau và máy bay bị trúng 2 viên đạn
Xác suất để 1 viên đạn trúng vào các bộ phận A,B,C,D lần lượt là 0,25; 0,25; 0,25; 0,25.
+) TH1: 2 viên đạn trúng 2 bộ phận liền kề
P(AB)+P(BA)+P(BC)+P(CB)+P(CD)+P(DC) = 6. P(AB) =6. O,25. 0,25= 0,375
+) TH2: 2 viên dạn cùng trúng vào một bộ phận
P(A)+P(B)+P(C)+P(D)= 4. P(A)= 4. $(0,25)^{2}$= 0,25
Vậy xác suất để máy bay rơi là: 0,375+0,25= 0,625 

Gọi N là trung diểm của BC, gọi O là trọng tâm $\Delta$ABC. Từ O dựng OS vuông góc với mp (ABC)
Trong mp (SAN) kẻ MG vuông góc với SN (1)
Ta có: BC vuông góc với AN
BC vuông góc với SO
=> BC vuông góc với (SAN) => BC vuông góc với MG (2)
(1)(2) => MG vuông góc với mp(SBC) => MG= d(M, (SBC))
Có: $\Delta$SNB vuông tại N=> $SN^{2}$ = $(2\sqrt{2})^{2}- a^{2}$
Có: $\Delta$ ANB vuông tại N => tan A= $\frac{BN}{AN}$ => AN= a/$\sqrt{3}$
Áp dụng hệ thức lượng với $\Delta$SAN: cosASN= $\frac{AS^{2}+SN^{2}-AN^{2}}{2.AS.SN}$= $\frac{4-\frac{a^{2}}{3}}{\sqrt{2}.\sqrt{8-a^{2}}}$ = cosMSG = $\frac{SG}{SM}$
=> SG= $\frac{4-\frac{a^{2}}{3}}{\sqrt{2}.\sqrt{8-a^{2}}}$. $\sqrt{2}$= $\frac{4-\frac{a^{2}}{3}}{\sqrt{8-a^{2}}}$
 Ta có: SGM là $\Delta$ vuô ngtại G => $MG^{2}$ = $SM^{2}-SG^{2}$= $\frac{a^{2}/9+ \frac{2a^{2}}{3}}{8- a^{2}}$
 => MG= $\sqrt{\frac{a^{2}/9+ \frac{2a^{2}}{3}}{8- a^{2}}}$

Theo giả thiết, số tự nhiên có 3 chữ số mà chữ số đằng sau lớn hơn chữ số đằng trước hay số đằng trước lớn hơn chữ số đằng sau, chính là số tự nhiên có 3 chữ số đôi một khác nhau. Gọi số tự nhiên đó là: $\overline{abc}$ (a,b,c đôi một khác nhau)
Ta thấy: a có 9 cách chọn
b có 9 cách chọn
c có 8 cách chọn
=> Số các số tự nhiên thỏa mãn là: 9.9.8= 648 số 

=3/2. $\int\limits_{2}^{3}$$\frac{2x+6}{x^{2}-4x-5}$.dx= 3/2. $\int\limits_{2}^{3}$$\frac{(2x-4)+10}{x^{2}-4x-5}$.dx= 3/2. $\int\limits_{2}^{3}$$\frac{(x^{2}-4x-5)^{'}}{x^{2}-4x-5}$.dx + 15. $\int\limits_{2}^{3}$$\frac{1}{x^{2}-4x-5}$.dx
 = 3/2. $\ln \left| {x^{2}-4x-5} \right|$ 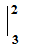+ 15. $\int\limits_{2}^{3}$$\frac{1}{(x-5)(x+1)}$.dx
 =3/2. $\ln \left| {x^{2}-4x-5} \right|$ 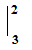+ 15. $\int\limits_{2}^{3}$$(\frac{1}{(x-5)}-\frac{1}{x+1})$.dx
 =3/2. $\ln \left| {x^{2}-4x-5} \right|$ 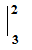+ 15. ($\ln \left| {x-5} \right|$- $\ln \left| {x+1} \right|$)
 = 3/2 $\ln 8/9$+ 15$\ln 1/2$

Điều kiện xác định của bất phương trình là: 5- x>0 và 3-x>0 => x<3
Với điều kiện đó, do tính nghịch biến của hàm số logarit cơ số 1/3, bất phương trình tương đương với $\sqrt{5-x}$ > 3-x. Bởi vậy, ta có thể viết:
BPT<=> $\begin{cases}x<3 \\ \sqrt{5-x}>3-x \end{cases}$
<=>$\begin{cases}x<3 \\ 5-x> 9-6x+x^{2} \end{cases}$
<=> $\begin{cases}x<3 \\ x^{2}-5x+4<0 \end{cases}$
<=>$\begin{cases}x<3 \\ (x-1)(x-4)<0 \end{cases}$
<=>$\begin{cases}x<3 \\ 1<x<4 \end{cases}$
Vậy x$\in $(1;3)

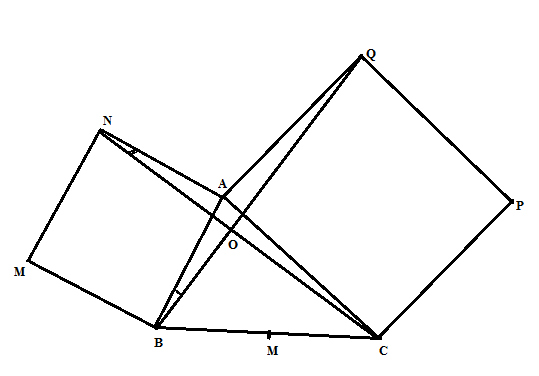$\widehat{BAQ}$= $\widehat{NAC}$ (=$\widehat{BAC}$+ $90^{0}$)
=> $\Delta$BAQ= $\Delta$NAC
=> BQ= NC và $\widehat{ABQ}$= $\widehat{ANC}$
Xét tứ giác MBON có: $\widehat{BON}$+ $\widehat{ONM}$+ $\widehat{NMB}$+ $\widehat{MBO}$= $\widehat{BON}$+ $\widehat{ONM}$+ $90^{0}$+ $90^{0}$+ $\widehat{ABQ}$= $\widehat{BON}$+ $90^{0}$+ $90^{0}$+ $\widehat{ONM}$+ $\widehat{ANC}$= $\widehat{BON}$+ $90^{0}$+ $90^{0}$+$90^{0}$= $360^{0}$ => $\widehat{BON}$= $90^{0}$
 Vậy BQ vuôgn góc với NC.

Xét $\Delta$ AH$A_{1}$ vuông tại H => AH= A$A_{1}$. sin$30^{0}$= a/2
=> $A_{1}H^{2}$= $a^{2}-a^{2}/4$= 3$a^{2}$/4 => $A_{1}H$= $\frac{a\sqrt{3}}{2}$
Trong $\Delta$ đều $A_{1}B_{1}C_{1}$ cạnh a có  $A_{1}H$= $\frac{a\sqrt{3}}{2}$ => H là trung điểm của $B_{1}C_{1}$=> $B_{1}C_{1}$ vuông góc với $A_{1}H$, mà AH vuông góc với $B_{1}C_{1}$ => $B_{1}C_{1}$ vuông góc với mp($A_{1}AH$)
 Trong mp($A_{1}AH$) kẻ HG vuông góc với $AA_{1}$
mà $B_{1}C_{1}$ vuông góc với mp($A_{1}AH$) => $B_{1}C_{1}$ vuông góc với HG
=> HG là đoạn vuông góc chung của  $AA_{1}$ và $B_{1}C_{1}$
Xét $\Delta$ $HGA_{1}$ vuông tại G có HG= AH. sin $HA_{1}G$= $\frac{a\sqrt{3}}{2}$. sin 30=  $\frac{a\sqrt{3}}{4}$

Gọi số có 6 chữ số là : $\overline{abcdef}$
TH1: a$\in $$\left\{ {1,2,3} \right\}$  => a có 3 cách chọn
                          Khi đó: b có 5 cách chọn
                                        c có 4 cách chọn
                                        d có 3 cách
                                        e có 2 cách
                                        f có 1 cách chọn
=> Có: 3.5.4.3.2.1= 360 số thỏa mãn
TH2: a=4 => a có 1 cách chọn, phân tiếp làm 2 trường hợp
TH2.1: b= $\left\{ {1,2} \right\}$  => b có 2 cách chọn
                         Khi đó: c có 4 cách chọn
                                      d có 3 cách chọn
                                      e có 2 cách chọn
                                      f có 1 cách chọn
=> Có: 2.4.3.2.1= 48 số thỏa mãn
TH 2.2: b=3, c=1 => b có 1 cách chọn, c có 1 cách chọn
                       Khi đó: d có 3 cách chọn
                                     e có 2 cách chọn
                                     f có 1 cách chọn
=> có 1.1.3.2.1= 6 số thỏa mãn
Vậy có: 360+48+6= 414 số thỏa mãn đề bài. 

a/ d1 có VTPT $\overrightarrow{n}$= (-1,2,3)
d2 có VTPT $\overrightarrow{m}$= (1,1,2)
=> $\left[ {\overrightarrow{m},\overrightarrow{n}} \right]$= (1,5,-3) $\neq $ $\overrightarrow{0}$
Vậy d1 và d2 chéo nhau.

Gọi I là trung điểm của AD
Vì $\Delta$SAD đều và (SAD) vuông góc với (ABCD) => SI vuông góc với (ABCD)
Từ I kẻ IH // DC => H là trung diểm của BC
Gắn hệ trục tọa độ vào hình vẽ sao cho I trùng gốc O, IH trùng Ox, ID trùng Oy, IS trùng Oz
Khi đó: I(0,0,0), C(a,a/2,0), P(a/2,a/2,0), M(a/2, -a/2, a/2), N(a/2,a/2,a/2)
=> $\overrightarrow{MN}$(0,a,0) => $MN^{2}=a^{2}$
$\overrightarrow{MP}$(0,a,-a/2) => $MP^{2}= a^{2}+a^{2}/4$
$\overrightarrow{NP}$=(0,0,-a/2) => $NP^{2}=a^{2}/4$
=> $\Delta$MNP vuông tại N=> $S_{MNP}$= 1/2. MN. NP= $\frac{a^{2}}{4}$
Lại có: $\left[ {\overrightarrow{MN},\overrightarrow{MP}} \right]$= (-1,0,0) (sau khi dã rút gọn a)
=> phương trình mp(MNP): -x+a/2=0
=> d(C, (MNP)) = $\frac{\left| {-a+ a/2} \right|}{\sqrt{(-1)^{2}}}$= a/2
=> $V_{CMNP}$ = 1/3. d(C, (MNP)). $S_{MNP}$= $\frac{a^{3}}{24}$

Lời giải này có yêu cầu trả vỏ sò để xem. Bạn hãy link trên để vào xem chi tiết

Ta thấy: $(3a)^{2}+(4a)^{2}=(5a)^{2}$ => $\Delta$ABC là tam giác vuông tại B => $S_{ABC}$= 1/2. AB. BC= 6$a^{2}$
$\Delta$ACB= $\Delta$ACD (c.c.c) => $S_{ABCD}$= 2. $S_{ABC}$= 12$a^{2}$
 Vậy $V_{S. ABCD}$= 1/3. SH. $S_{ABCD}$ = $\frac{36a^{3}}{7}$

Thiết diện qua M và song song với mp(SBC) nên trong mp(ABCD) kẻ MN// BC cắt CD tại N.
Trong mp(SAB) kẻ MH// SB cắt AS tại H.
Trong mp(SAD), từ H kẻ HG// AD cắt SD tại G.
Khi đó thiết diện (P) cần tìm chính là mp(MHGN)
Ta thấy, MN// BC => MN vuông góc với AB mà MN vuông góc với SA => MN vuông góc với mp(SAB) => MN vuông góc với MH
Do vậy thiết diện là hình thang vuông tại M và H có HG// MN
Có: BA=BC=a => $\Delta$BAC là tam giác vuông cân tại B => $\widehat{BAC}$= $45^{0}$ => $\widehat{CAD}$ = $45^{0}$
=> AD là cạnh huyền trong $\Delta$CAD vuông cân tại C có CA= a.$\sqrt{2}$ => AD= 2a
Gọi I= AC $\cap $MN, ta có:
MI/BC= AM/AB => MI= a
NI/DA= CN/CD= BM/BA = $\frac{a-x}{a}$ => NI= 2.(a-x)
=> MN= 3a- 2x
Mặt khác, $\Delta$SHG $\sim $ $\Delta$SAD => HG/AD= SH/SA =BM/BA = $\frac{a-x}{a}$ => HG= 2.(a-x)
Có: $\Delta$AMH $\sim $ $\Delta$ABS => AH/AS= AM/AB =>AH= $\frac{x. a\sqrt{2}}{a}$ => MH= $\sqrt{AH^{2}+AM^{2}}$= $\sqrt{3}$.x
Vậy: $S_{MNHG}$ = 1/2.(HG+MN). HM =  $\frac{(5a-4x).\sqrt{3}x}{2}$

Trong mp(SAC) kẻ AC' vuông góc với SC (1)
Trong mp(SAB) kẻ AB' vuông góc với SB. Lại có: BC vuông góc với (SAB)
=> AB' vuông góc với (SBC) => AB' vuông góc với SC (2)
Trong mp(SAD) kẻ AD' vuông góc với SD. Lại có: DC vuông góc với (SAD)
=> AD' vuông góc với (SDC) => AD' vuông góc với SC (3)
(1)(2)(3) => SC vuông góc với mp(AB'C'D'). Như vậy mp(AB'C'D') chính là thiết diện ($\alpha$) cần tìm.
Ta có: $\Delta$SB'A = $\Delta$SD'A (g.c.g) => AB'= AD' (4)
Lại có: $\Delta$SC'B' = $\Delta$SC'D' (c.g.c) => C'B'= C'D' (5)
(4)(5)=> $\Delta$AB'C' = $\Delta$AD'C'
=> 2 đường chéo của tứ giác AB'C'D' vuông góc với nhau
=> $S_{AB'C'D'}$ = 1/2. AC'. B'D'
Có: AC' là đường cao trong $\Delta$SAC vuông tai A => $\frac{1}{AC'^{2}}$= $\frac{1}{AS^{2}}+\frac{1}{AC^{2}}$ => AC'= a. $\sqrt{\frac{2}{3}}$
Lại có: AB' là đường cao trong $\Delta$SAB vuông tai A => $\frac{1}{AB'^{2}}$= $\frac{1}{AS^{2}}+\frac{1}{AB^{2}}$ => AB'= $\frac{a}{\sqrt{2}}$
$\Delta$SB'A vuông tai B' => SB'= $\frac{a}{\sqrt{2}}$
Có: SB=SD, SB'=SD' => $\frac{SB'}{SB}$= $\frac{SD'}{SD}$ => $\Delta$SB'D' đồng dạng với $\Delta$SBD
=> B'D'/BD= SB'/SB= $\frac{\frac{a}{\sqrt{2}}}{a\sqrt{2}}$= 1/2 => B'D' = $\frac{a\sqrt{2}}{2}$
Như vậy: $S_{AB'C'D'}$ = 1/2. a. $\sqrt{\frac{2}{3}}$. $\frac{a\sqrt{2}}{2}$ = $\frac{a^{2}}{2\sqrt{3}}$