BC=a, AC=b, AB= c
Có: $\begin{cases}b^{2}= c^{2}+a^{2}- 2ca. cosB \\ c^{2}= a^{2}+ b^{2}- 2ab. cosC \end{cases}$
=> $\begin{cases}b^{2}- c^{2}= 121- 22c. cos35 (1)\\ c^{2}- b^{2}= 121- 22b. cos70 (2) \end{cases}$
=> 11- 2c.cos35= 2b. cos70- 11
=> 11= b. cos70+ c. cos35 (3)
Thế (3) vào (1) hoặc (2) để giải tiếp nhé :)

Khai triển nhị thức Newton: $(1+x+x^{2}+x^{3})^{15}$
= $C^{k}_{15}$. $(x+x^{2}+x^{3})^{k}$
= $C^{k}_{15}$. $C^{t}_{k}$. $x^{k-t}$ $(x^{2}+x^{3})^{t}$
= $C^{k}_{15}$. $C^{t}_{k}$. $x^{k-t}$. $C^{m}_{t}$ $(x^{})^{2m}$. $x^{3.(t-m)}$
 = $C^{k}_{15}$. $C^{t}_{k}$. $C^{m}_{t}$. $x^{k+2t-m}$
Khi đó ta cần tìm (k,t,m) sao cho: k+2t-m=0, k$\leqslant $ 15, t$\leqslant $k, m$\leqslant $t
=> (k,t,m)= $\left\{ {(4,3,0),(4,4,2),(5,3,1),(5,4,3),(5,5,5),(6,2,0),(6,3,2),(6,4,4),(7,2,1),(7,3,3),(8,1,0),(8,2,2),(9,1,1),(10,0,0)} \right\}$
Vậy hệ số của $x^{10}$ trong khai triển là: 1392456

Đồng nhất hình vẽ với hệ tọa độ trong không gian sao cho A' là gốc tọa độ, A'B; trùng Ox, A'D' trùng Oy, A'A trùng Oz
Khi đó, A'(0,0,0), M(1/2,0,0), N(1,1/2,1), P(0,1,1/2), A(0,0,1), C'(1,1,0)
Ta có: $\overrightarrow{AC}$= (1,1,-1)
$\overrightarrow{MN}$= (1/2,1/2,1)= (1,1,2)
$\overrightarrow{MP}$= (-1/2,1,1/2)= (-1,2,1)
=> Vector pháp tuyến $\overrightarrow{n}$ của mp(MNP) là: $\left[ {\overrightarrow{MN},\overrightarrow{MP}} \right]$= (-3,-3,3)
Ta thấy tọa độ của $\overrightarrow{n}$ tỉ lệ với tọa độ của $\overrightarrow{AC}$ => AC' vuông góc với mp(MNP) -đpcm

Lời giải này có yêu cầu trả vỏ sò để xem. Bạn hãy link trên để vào xem chi tiết

Áp dụng công thức: 1+ $(tan(x))^{2}$= $\frac{1}{(cos(x))^{2}}$ với x$\neq $$\Pi/2$+k$\Pi$ (k$\in $Z)
Có: tan x= 3/2 => $(cos(x))^{2}$= 4/13 => cos x= $\pm $$\sqrt{4/13}$
Có: tan x= $\frac{sin x}{cos x}$= 3/2 => sin x= $\frac{3}{2}$. ($\pm $$\sqrt{\frac{4}{13}}$)
Có: 1+ $(cot(x))^{2}$= $\frac{1}{(sin(x))^{2}}$ với x$\neq $k$\Pi$ (k$\in $Z) => $(cot(x))^{2}$= $\frac{4}{9}$ => cot x= $\pm \frac{2}{3}$

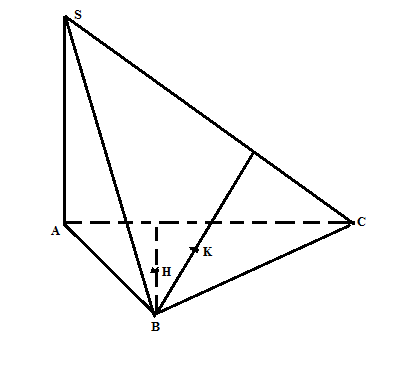a/ +)K là trực tâm $\Delta$ SBC => SC vuông góc với BK
H là trực tâm $\Delta$ ABC=> BH vuông góc với SC
=> SC vuông góc với (BHK)
+) SC vuông góc với BK
SA vuông góc với BH
=> (SAC) vuông góc với (BHK)

b/ $\Delta$ SB'A đồng dạng với $\Delta$SAB (g-g)
=> $\frac{SB'}{SA}$=$\frac{SA}{SB}$ => SB'. SB= $SA^{2}$
$\Delta$ SC'A đồng dạng với $\Delta$SAC (g-g)
=> $\frac{SC'}{SA}$=$\frac{SA}{SC}$ => SC'. SC= $SA^{2}$
$\Delta$ SD'A đồng dạng với $\Delta$SAD (g-g)
=> $\frac{SD'}{SA}$=$\frac{SA}{SD}$ => SD'. SD= $SA^{2}$
=> đpcm

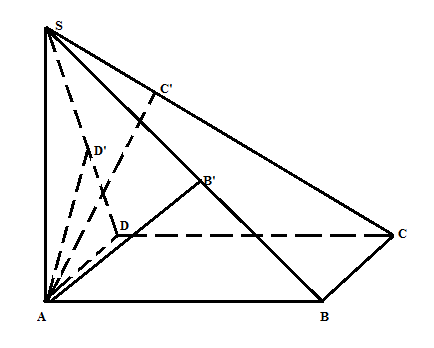a/ SC vuông góc với mp(AB'C'D') => SC vuông góc với AB'
Lại có BC vuông góc với AB' ( do BC vuông góc với mp( SAB))
=> AB' vuông góc với mp(SBC) => AB' vuông góc với SB
Tương tự: AD' vuông góc với mp( SDC) => AD' vuông góc với SD

Số hạng tổng quát khi khai triển là: $C^{k}_{4}$. $(2x- x^{2})^{k}$= $C^{k}_{4}$. $C^{t}_{k}$. $(2x)^{k-t}$. $(-x^{2})^{t}$= $(-1)^{t}$. $C^{k}_{4}$. $C^{t}_{k}$. $2^{k-t}$. $x^{k+t}$ với k$\leq $4, t$\leq $k
Khai triển chứa $x^{7}$ => k+t=7 và thỏa mãn 2 điều kiện trên
=> k=4, t=3
=> Hệ số của số hạng chứa $x^{7}$ trong khai triển là: (-1). $C^{4}_{4}$. $C^{3}_{4}$. $2^{1}$= -8

Số hạng tổng quát của khai triển là: $C^{k}_{8}$. $x^{2k}$. $C^{t}_{k}$. $1^{k-t}$. $(-x)^{t}$= $(-1)^{t}$. $C^{k}_{8}$. $C^{t}_{k}$. $x^{2k+t}$ với t$\leq $k
$x^{8}$ trong khai triển => 2k+t= 8
=> (k,t)= $\left\{ {(3,2), (4,0)} \right\}$
=> Hệ số số hạng khai triển $x^{8}$ là: $C^{3}_{8}$+ $C^{4}_{8}$

c/ $S_{OMN}$=16 => OM.ON=32 => a.b=32 => b=32/a
=> M(a,0), N(0, 32/a) => $\overrightarrow{MN}$( -a, 32/a) => MN= $\sqrt{a^{2}+(32/a)^{2}}$
MN: 32/a. (x-2)+ a. (y-4)=0
Khi đó: d(O, MN)= $\frac{\frac{-64}{a}-4a}{\sqrt{(32/a)^{2}+a^{2}}}$
=> $S_{OMN}$= 1/2. d(O, MN). MN= $\frac{-32}{a}$ - 2a = 16
=> a=-4, b=-8
=> $\overrightarrow{MN}$=(4,-8)= (1,-2)
=> MN:2x+y+8=0

M$\in $Ox => M(a,0)
N$\in $Oy => N(0,b)
a/ A(2,4) là trung điểm => $\begin{cases}\frac{a+0}{2}=2 \\ \frac{0+b}{2}=4 \end{cases}$
=> a=4, b=8
=> $\overrightarrow{MN}$=( -4,8)= (-1,2)
=> MN: 2x+y-8=0

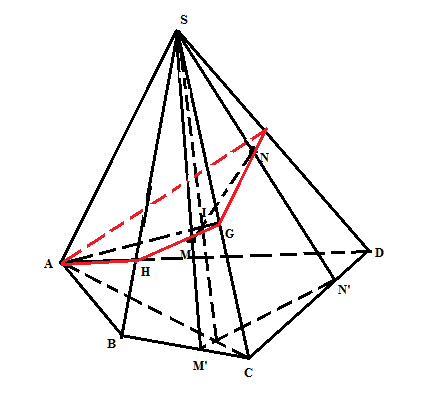Gọi M' =SM$\cap $BC, N'= SN$\cap $CD
Trong mp( ABCD), gọi O= M'N'$\cap $AC
Trong mp( SM'N') gọi I= MN$\cap $SO
Trong mp( SAC) gọi G= AI$\cap $SC
Trong mp( SCD) gọi T= GN$\cap $SD
Trong mp( SBC) gọi H= GM$\cap $SB
Vậy thiết diện của mp(SMN) với hình chóp là (AHGT).

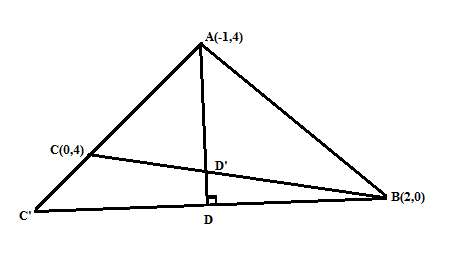a/ $\overrightarrow{AB}$=(3,-4) => AB=5
$\overrightarrow{AC}$=(1,0) =>AC=1
=>AC<AB
Phương trình đường AC: -y+4=0
Trên AC lấy C' => C' có tọa độ (x,4) sao cho AC'=5
$\overrightarrow{AC'}$=( x+a,0)
=> $\left| {x+1} \right|$=5 => x=4 hoặc x=-6
Trường hợp x=-6 loại vì khi đó $\overrightarrow{AC'}$ ngược chiều với $\overrightarrow{AC}$
Khi AD là phân giác trong thì D sẽ là trung điểm của BC'=> D(3,2)
=> $\overrightarrow{AD}$(4,-2)= (2,-1)
=> AD: x+2y-7=0
b/ Gọi D' là chân đường phân giác trong của AD=> D' = BC$\cap $AD
Mà $\overrightarrow{BC}$=(2,-4)=(1,-2)
=> BC: 2x+y-4=0
=> D'(1/3,10/3)