|
|
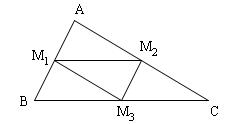
Biết $M_1(2;1),M_2(5;3),M_3(3,-4)$
-Phương trình đường thẳng $M_1M_2 :$
$\frac{x-2}{5-2}=\frac{y-1}{3-1} \Leftrightarrow 2x-3y-1=0$
$BC//M_1M_2$nên phương trình $BC$ có dạng $2x-3y+C=0$, đường thẳng $BC$ qua $M_3(3,-4)$
$\Rightarrow 6+12+C=0\Rightarrow C=-18$
-Phương trình cạnh $BC$ của tam giác là $2x-3y-18=0$
-Phương trình đường thẳng $M_2M_3 :$
$\frac{x-5}{3-5}=\frac{y-3}{-4-3} \Leftrightarrow 7x-2y-29=0$
$AB//M_2M_3$ nên phương trình đường thẳng $AB$ có dạng : $7x-2y+C=0$
$AB$ qua $M_1(2,1)\Rightarrow 14-2+C=0\Rightarrow C=-12$
Phương trình cạnh $AB$ của tam giác là : $7x-2y-12=0$
- Phương trình đường thẳng $M_1M_3 :$
$\frac{x-2}{3-2}=\frac{y-1}{-4-1} \Leftrightarrow 5x+y-11=0$
Phương
trình cạnh $AC//M_1M_3$ nên phương trình cạnh $AC$ có dạng $5x+y+C=0$
đường này qua $M_2(5;3)\Rightarrow 25+3+C=0\Rightarrow C=-28$
Phương trình cạnh $AC$ của tam giác là $5x-y-28=0$
|