|
|
$1$) Đặt $t = {2^x},t > 0$ ta có :
$\begin{array}{l}
\,\,\,\,\,\,\,\,\,\,\,{4^x} - {5.2^x} + m \le
0\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,(1)\\
\Leftrightarrow \,\,\,\,\,f(t) = {t^2} - 5t + m \le
0\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,(2)\\
\,\,\,\,\,\Delta = 25 - 4m,\,\,\,\Delta = 0\,\,\, \Leftrightarrow m = \frac{{25}}{4}
\end{array}$
$a)\,\,m > \frac{{25}}{4}:\,\,\,\,\,\Delta < 0:$(2) vô nghiệm, do đó $f(t) > 0,\forall t$
$ \Rightarrow $($1$) vô nghiệm
$\begin{array}{l}
b)\,\,\,m = \frac{{25}}{4}:\,\,\Delta = 0:\,\,{t_1} = {t_2} = \frac{5}{2}\\
\end{array}$
$f(t) = {\left( {t - \frac{5}{2}} \right)^2}\,\,\, \Rightarrow (1)$ có nghiệm là $x = {\log _2}\frac{5}{2}$
$c)\,\,m < \frac{{25}}{4}:\,\,\,f(t)$có dấu trên $R$
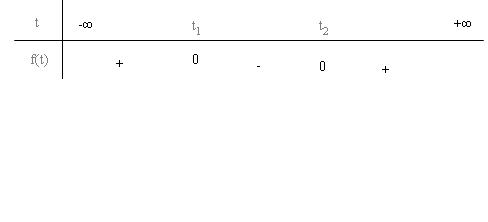
Do $S = {t_1} + {t_2} = 5 > 0$nên ít nhất $f(t)$có một nghiệm dương:$\left[ \begin{array}{l}
{t_1} \le 0 < {t_2}\\
0 < {t_1} < {t_2}
\end{array} \right.$
Tập nghiệm của (2) là :$\left( {0,{t_2}} \right]\,\,\,$hoặc$\left[ {{t_1},{t_2}} \right]$
Và do đó :$\left[ \begin{array}{l}
0 < {2^x} \le {t_2}\\
{t_1} \le {2^x} \le {t_2}
\end{array} \right.$
Suy ra: $m \le \frac{{25}}{4}$thì bất phương trình ($1$) có nghiệm
$2$) $\forall x \in \,R\,$bất phương trình có nghiệm
$3$) $\forall x \in \,R\,$ bất phương trình có nghiệm
$4) \,\,m \le - 2$
|