Bài 103718

Question

$1)$ Lập bảng biến thiên và vẽ đồ thị (

$C$ ) hàm số từ đường (

$C$ ), suy ra đồ thị

$({C^,})$ của hàm
số

$y = {\log _2}\left( {x + 1} \right)$

$2)$ Từ

$({C^,})$ , suy ra đồ thị

$({C_1})$ của hàm số

$y = \left| {{{\log }_2}\left( {x + 1} \right)} \right|$

$3$ ) chứng minh rằng đồ thị

$({C_2})$ của hàm số

$y = {\log _2}\left| {x + 1} \right|$ nhận đường thẳng

$x = - 1$ làm trục đối xứng. Vẽ

$({C_2})$

score 0 · Answer 1

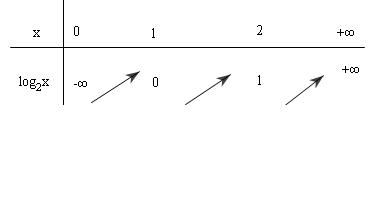
1 Hàm số

$y = {\log _2}x$ đồng biến trong khoảng

$\left( {0,\, + \infty } \right)$ . Bảng biến
thiên và đồ thị:

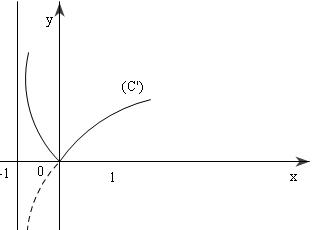
$\forall M\left( {x,\,y} \right) \in \left( C \right)\,$ và

$M'\left( {x',\,y'} \right) \in \left( {c'} \right)\,sao\,cho\,\,y' = y$ ta có

$y' = y \Leftrightarrow {\log _2}\left( {x' + 1} \right) = {\log _2}x \Leftrightarrow x' + 1 = x \Leftrightarrow x' - x = - 1 \Leftrightarrow \overrightarrow {MM'} = \overrightarrow {i.}$

$\overrightarrow i$ là véc tơ đơn vị của trục hoành

$Ox$ . Hệ thức chứng tỏ

$M’$ là điểm tịnh tiến của

$M$ bởi phép tịnh tiến theo véc tơ -

$\overrightarrow i$ . Suy ra

$C'$ là tịnh tiến của (

$C$ ) bởi phép
tịnh tiến trên.

$2$ ) Ta có:

$y = \left| {{{\log }_2}\left( {x + 1} \right)} \right| = \left\{ \begin{array}{l} {\log _2}x + 1\,\,\,\,\,\,\,\,\,\,\,x \ge 0\\ - {\log _2}\left( {x + 1} \right)\,\,\,\, - 1 < x < 0 \end{array} \right.$
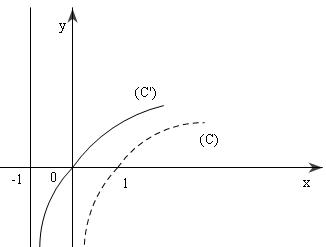
Do đó: trong nửa mặt phẳng

$x \ge 0$ phần của

$({C_1})$ và

$C'$ trùng nhau, trong nửa mặt
phẳng

$x < 0$ , đối xứng nhau qua

$Ox$ .

$3)$ Xét

$f(x) = \,{\log _2}\left| {x + 1} \right|$

$\begin{array}{l} \forall \alpha \ne 0:\,f( - 1 + \alpha ) = f\left( { - 1 + \alpha + 1} \right) = f\left( \alpha \right) = {\log _2}\left| \alpha \right|\\ f\left( { - 1 - \alpha } \right) = f\left( { - 1 - \alpha + 1} \right) = f\left( { - \alpha } \right) = {\log _2}\left| { - \alpha } \right| = {\log _2}\left| \alpha \right|\\ \forall \alpha \ne 0:\,f\left( { - 1 + \alpha } \right) = f\left( { - 1 - \alpha } \right) \end{array}$
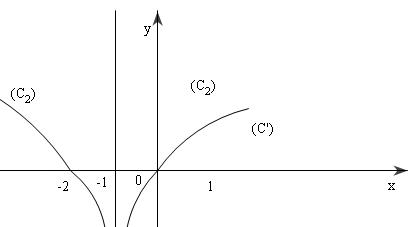
Do đó đồ thị hàm số

${\log _2}\left| {x + 1} \right|$ nhận đường thẳng

$x = - 1$ làm trục đối xứng.
Đồ thị

$({C_2})$ chính là

$C'$ . Phần còn lại đối xứng với

$C'$ qua trục đối xứng

$x = - 1$