|
|
$1)$..Cho hàm số xác định $\forall x > 0$
$\begin{array}{l}
f(x)\, = \,9{x^2}\ln x + 3{x^2} - 36\ln x - 36 - 21{x^2} + 108\\
= 9{x^2}\ln x - 36\ln x - 18{x^2} + 72\\
= 9\left( {{x^2} - 4} \right)\left( {\ln x - 2} \right)\\
\left\{ \begin{array}{l}
f'(x) = 0\\
x > 0
\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}
x = 2\\
x = {e^2}
\end{array} \right.\\
\end{array}$
Bảng biến thiên:
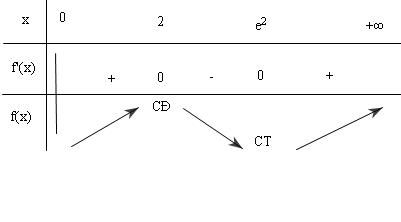
Hàm số tăng trong khoảng $\left( {0,\,\,\,2} \right),\,\,\,\left( {{e^2},\,\,\, + \infty } \right)$ và
giảm trong khoảng $\left( {2,\,\,{e^2}} \right)$
$2)$ $f'(x)=9x^2 \ln x+3x^2-81 \ln x-81-30x^2+324$
$=9 \ln x(x^2-9)-27(x^2-9)$
$=9(x^2-9)(\ln x-3)$
$f'(x)=0 \Leftrightarrow \begin{cases}x>0 \\ \left[ \begin{gathered} x=3 \\ x=e^3 \end{gathered} \right. \end{cases} $
$\Leftrightarrow \left[ \begin{gathered} x=3 \\ x=e^3 \end{gathered} \right. $
Hàm số tăng trong 2 khoảng $\left( {0,\,\,3} \right),\,\,\,\left( {{e^3},\,\, + \infty }
\right)$ và giảm trong khoảng $\left( {3,\,\,{e^3}} \right)$

|