|
|
Hàm số xác định $\forall x > 0$ và $x \ne 1$
${y^ / } = \frac{{\ln x - 1}}{{{{\ln }^2}x}},\,\,\,\,\,{y^ / } = 0\,\,\,\,\, \Leftrightarrow
\,\,\,x = e$
Dấu ${y^ / }$:
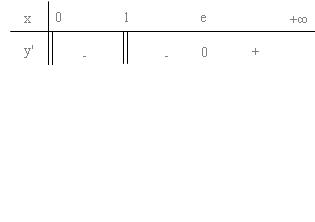
Hàm số đạt cực tiểu tại điểm $\left\{ \begin{array}{l}
x = e\\
{y_{CT}} = e
\end{array} \right.$
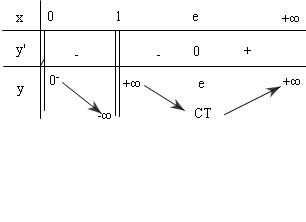
$\mathop {\lim }\limits_{x \to {0^ + }} y = {0^ - },\,\,\,\,\mathop {\lim }\limits_{x \to 1} y =
\pm \infty \,\,\, \Rightarrow $ đường $x = 1$là tiệm cận đứng
$\mathop {\lim }\limits_{x \to + \infty } y = + \infty $
Bảng biến thiên:
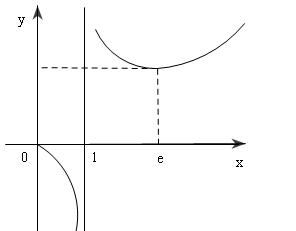
Đồ thị :
|