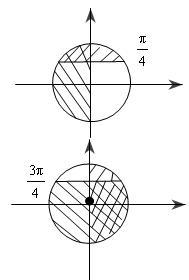
$cosx – sinx – cos2x > 0\Leftrightarrow (\cos x-\sin )-(cos^2x-sin^2x)>0$
$\Leftrightarrow (cosx-sinx)(1-(cosx+sinx))>0$
$\Leftrightarrow \sqrt{2}cos(x+\frac{\pi}{4} ) (1-\sqrt{2}sin(x+\frac{\pi}{4} ) )>0$
Đặt $t=x+\frac{\pi}{4} $ ta được $\sqrt{2}cost(\sqrt{2}sint-1 )<0 $
$\left[ \begin{array}{l}\begin{cases}cost>0\\ sint<\frac{1}{\sqrt{2} } \end{cases} \\\begin{cases}cost<0 \\ sint>\frac{1}{\sqrt{2} } \end{cases} \end{array} \right. \Leftrightarrow \left[ \begin{array}{l}-\frac{\pi}{2}+k2\pi<t<\frac{\pi}{4}+2k\pi \\\frac{\pi}{2}+2k\pi<t<\frac{3\pi}{4}+2k\pi \end{array} \right. $
$\Leftrightarrow \left[ \begin{array}{l}-\frac{3\pi}{4}+2k\pi<x<2k\pi \\\frac{\pi}{4}+2k\pi<x<\frac{\pi}{2}+2k\pi \end{array} \right. $
Kết hợp $
x\in[0;2\pi]\Rightarrow\left[\begin{array}{I}\frac{5\pi}{4}<x<2\pi\\\frac{\pi}{4}<x<\frac{\pi}{2}\end{array}\right.$