CÁC PHƯƠNG PHÁP GIẢI TOÁN CỰC TRỊ HÌNH HỌC BẰNG VECTOR

Trong chuyên đề này, ta sẽ đề cập đến các phương pháp giải toán cực trị hình học bằng vector:
1.    Tìm cực trị nhờ đánh giá độ dài vector
2.    Tìm cực trị nhờ đánh giá bình phương vô hướng
3.    Tìm cực trị nhờ đánh giá tích vô hướng của hai vector
Cách áp dụng cụ thể sẽ được nói trong từng phương pháp.

Phương pháp 1: Tìm cực trị nhờ đánh giá độ dài vector
Ví dụ 1.1:
Cho tam giác nhọn ABC nội tiếp đường tròn (O). Tìm điểm M thuộc đường tròn (O) để biểu thức sau đạt GTLN, GTNN:
                        $T = |\overrightarrow {MA}  + \overrightarrow {MB}  - \overrightarrow {MC|}$
Giải:
Gọi I là đỉnh thứ tư của hình bình hành ACBI thì: $\overrightarrow {IA}  + \overrightarrow {IB}  - \overrightarrow {IC}  = \overrightarrow 0$
                          
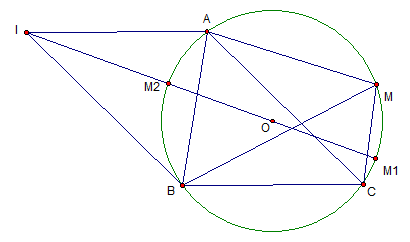
Khi đó : $\overrightarrow {MA}  + \overrightarrow {MB}  - \overrightarrow {MC}  = (\overrightarrow {MI}  + \overrightarrow {IA} ) + (\overrightarrow {MI}  + \overrightarrow {IB} ) - (\overrightarrow {MI}  + \overrightarrow {IC} )$
                                        $= \overrightarrow {MI}  + \overrightarrow {IA}  + \overrightarrow {IB}  - \overrightarrow {IC}$
                                        $= \overrightarrow {MI}$
Như vậy T lớn nhất $\Leftrightarrow$$|\overrightarrow {MI} |$ lớn nhất $\Leftrightarrow$MI lớn nhất $\Leftrightarrow$M $\equiv$ ${M_1}$ với ${M_1}$ là giao điểm của OI với đường tròn (O), ${M_1}$ nằm ngoài đoạn OI..
Tương tự T nhỏ nhất $\Leftrightarrow$$M \equiv {M_2}$ với ${M_2}$ là giao điểm của OI với đường tròn (O) , ${M_2}$ thuộc đoạn OI.

Ví dụ 1.2:
Cho tam giác nhọn ABC nội tiếp (O) và ba số$\alpha ,\beta ,\gamma$ sao cho $\alpha  + \beta  + \gamma  \ne 0$. Tìm điểm M thuộc (O) để biểu thức sau đạt GTLN, GTNN
                               $T = |\alpha \overrightarrow {MA}  + \beta \overrightarrow {MB}  + \gamma \overrightarrow {MC} |$
Giải:
Gọi I là tâm tỷ cự của hệ điểm A, B, C ứng với các hệ số $\alpha ,\beta ,\gamma$
$\alpha \overrightarrow {MA}  + \beta \overrightarrow {MB}  + \gamma \overrightarrow {MC}  = \alpha (\overrightarrow {MI}  + \overrightarrow {IA} ) + \beta (\overrightarrow {MI}  + \overrightarrow {IB} ) + \gamma (\overrightarrow {MI}  + \overrightarrow {IC} )$
                                    $= (\alpha  + \beta  + \gamma )\overrightarrow {MI}  + \alpha \overrightarrow {IA}  + \beta \overrightarrow {IB}  + \gamma \overrightarrow {IC}$
                                    $= (\alpha  + \beta  + \gamma )\overrightarrow {MI}$
Do đó $T = |(\alpha  + \beta  + \gamma )|.MI$.
Gọi ${M_1},{M_2}$ lần lượt là giao của OI với đường tròn (O) trong đó $I{M_1} \geqslant I{M_2}$ thì :
 T lớn nhất khi và chỉ khi M trùng ${M_1}$
 T nhỏ nhất khi và chỉ khi M trùng ${M_2}$

Ví dụ 1.3:
Cho đường tròn (O) và hai điểm phân biệt A, B cố định sao cho đường thẳng AB không cắt (O). Tên đường tròn đó lấy điểm C và dựng điểm M thỏa điều kiện $\overrightarrow {CM}  = \overrightarrow {CA}  + \overrightarrow {CB}$. Tìm vị trí của điểm C để đoạn CM có độ dài nhỏ nhất, lớn nhất.
Giải :
Gọi I là trung điểm AB thì I cố định và $\overrightarrow {CM}  = 2\overrightarrow {CI}$.
Gọi ${C_1},{C_2}$ là giao của OI với đường tròn (O) và coi $I{C_1} \geqslant I{C_2}$.
                  
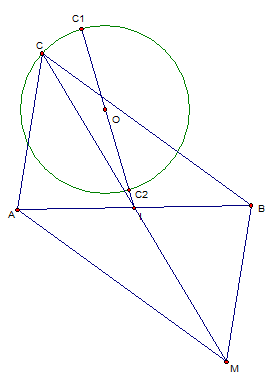
Với C bất kì thuộc (O) ta có:
$IC + CO \geqslant IO = O{C_1} + O{C_2}$
Do đó $IC \geqslant I{C_2}$. Dấu “=” xảy ra khi và chỉ khi C trùng ${C_2}$
Mặt khác $IC \leqslant IO + OC = IO + O{C_1} = I{C_1}$
Do đó $IC \leqslant I{C_1}$. Dấu “=” xảy ra khi và chỉ khi C trùng ${C_1}$
 Vậy CM lớn nhất khi và chỉ khi C trùng ${C_2}$
         CM nhỏ nhất khi và chỉ khi C trùng ${C_1}$

Ví dụ 1.4:
Giả sử tam giác ABC và A’B’C’ là các tam giác thay đổi, có trọng tâm G và G’ cố định. Tìn GTNN của tổng:
                   $T = AA' + BB' + CC'$
Giải:
Vì $\overrightarrow {GA}  + \overrightarrow {GB}  + \overrightarrow {GC}  = \overrightarrow 0$ và $\overrightarrow {G'A'}  + \overrightarrow {G'B'}  + \overrightarrow {G'C'}  = \overrightarrow 0$ nên
$\overrightarrow {AA'}  + \overrightarrow {BB'}  + \overrightarrow {CC'}  = \overrightarrow {AG}  + \overrightarrow {GG'}  + \overrightarrow {G'A}  + \\ \overrightarrow {BG}  + \overrightarrow {GG'}  + \overrightarrow {G'B'}  + \overrightarrow {CG}  + \overrightarrow {GG'}  + \overrightarrow {G'C'}$
                           $= 3\overrightarrow {GG'}  - (\overrightarrow {GA}  + \overrightarrow {GB}  + \overrightarrow {GC} ) + (\overrightarrow {G'A'}  + \overrightarrow {G'B'}  + \overrightarrow {G'C'} )$
                           $= 3\overrightarrow {GG'}$
Do đó:
$AA' + BB' + CC' = |\overrightarrow {AA'} | + |\overrightarrow {BB'} | + |\overrightarrow {CC'} |$
                              $\geqslant |\overrightarrow {AA'}  + \overrightarrow {BB'}  + \overrightarrow {CC'} |$
                               $= 3|\overrightarrow {GG'} | = 3GG'$
Đẳng thức xảy ra khi và chỉ khi các vector $\overrightarrow {AA'} ,\overrightarrow {BB'} ,\overrightarrow {CC'}$ cùng hướng
Vậy min$AA' + BB' + CC'$= 3GG’
Nhận xét: từ khái niệm trọng tâm của đoạn thẳng và tứ giác ta cũng có:
Min ( AA’+BB’) = 2GG’
Min ( AA’+BB’+CC’+DD’) = 4 GG’

Phương pháp 2: Tìm cực trị nhờ đánh giá bình phương vô hướng:
Ví dụ 2.1:
Cho tam giác ABC và đường thẳng d cố định đi qua C. Trên d lấy điểm M và lập tổng $3M{A^2} + 2M{B^2}$. Tìm vị trí M để tổng đó đạt giá trị nhỏ nhất.
Giải:

Giả sử I là điểm sao cho $3\overrightarrow {IA}  + 2\overrightarrow {IB}  = \overrightarrow 0$ thì I là điểm cố định .
                   
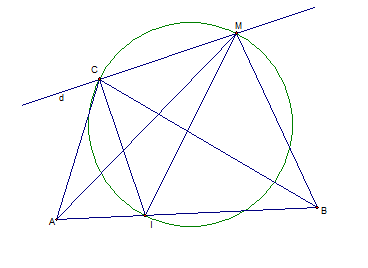
Ta có $3M{A^2} + 2M{B^2} = 3{(\overrightarrow {MI}  + \overrightarrow {IA} )^2} + 2{(\overrightarrow {MI}  + \overrightarrow {IB} )^2}$
                                    $= 5M{I^2} + 3I{A^2} + 2I{B^2}$
Do đó $3M{A^2} + 2M{B^2}$ nhỏ nhất khi và chỉ khi MI nhỏ nhất $\Leftrightarrow$$MI \bot d$, điều này tương đương $\widehat {IMC} = {90^0}$, tức là M thuộc đường tròng (C) đường kính IC.
Vậy $3M{A^2} + 2M{B^2}$ nhỏ nhất khi và chỉ khi M là giao điểm của d với đường tròn đường kính IC

Ví dụ 2.2:
Trong mọi tam giác ABC nội tiếp đường tròn (O) tìm tam giác có tổng         T = ${a^2} + {b^2} + {c^2}$ lớn nhất.
Giải:
Ta có:
                       $T = B{C^2} + C{A^2} + A{B^2}$
                          $= (\overrightarrow {OC}  - \overrightarrow {OB} ) + (\overrightarrow {OA}  - \overrightarrow {OC} ) + (\overrightarrow {OB}  - \overrightarrow {OA} )$
                          $= 6{R^2} - 2(\overrightarrow {OC} .\overrightarrow {OB}  + \overrightarrow {OA} .\overrightarrow {OC}  + \overrightarrow {OB} .\overrightarrow {OA} )$
                          $= 9{R^2} - {(\overrightarrow {OA}  + \overrightarrow {OB}  + \overrightarrow {OC} )^2} = 9{R^2} - 9O{G^2}$
Suy ra T$\leqslant 9{R^2}$. Đẳng thức xảy ra $\Leftrightarrow O \equiv G \Leftrightarrow$ ABC là tam giác đều
Vậy trong mọi tam giác ABC nội tiếp đường tròn thì tam giác đều thỏa mãn bài toán.

Ví dụ 2.3:
Trong mọi tam giác ABC nội tiếp đường tròn (O), hãy tìm tam giác có tổng bình phương các khoảng cách từ tâm đường tròn đến các cạnh là nhỏ nhất.
Giải:
Gọi ${d_a},{d_b},{d_c}$ lần lượt là khoảng cách từ tâm đường tròn đến ba cạnh BC, CA, AB của tam giác.
                              
Ta có:
${d_a}^2 + {d_b}^2 + {d_c}^2 = ({R^2} - \frac{{{a^2}}}{4}) + ({R^2} - \frac{{{b^2}}}{4}) + ({R^2} - \frac{{{c^2}}}{4})$
                                  $= 3{R^2} - \frac{1}{4}({a^2} + {b^2} + {c^2})$
                                  $\geqslant 3{R^2} - \frac{1}{4}.9{R^2} = \frac{{3{R^2}}}{4}$
Đẳng thức xảy ra khi và chỉ khi tam giác ABC đều.
Vậy min $({d_a}^2 + {d_b}^2 + {d_c}^2) = \frac{{3{R^2}}}{4}$ khi và chỉ khi tam giác ABC đều.

Ví dụ 2.4:
Cho điểm M nằm trong mặt phằng tam giác ABC. Tìm giá trị nhỏ nhất của biểu thức $T = M{A^2} + M{B^2} + M{C^2}$
Giải :  
Gọi G là trọng tâm của tam giác ABC, ta có
            $T = {(\overrightarrow {MG}  + \overrightarrow {GA} )^2} + {(\overrightarrow {MG}  + \overrightarrow {GB} )^2} + {(\overrightarrow {MG}  + \overrightarrow {GC} )^2}$
               $= 3M{G^2} + G{A^2} + G{B^2} + G{C^2} + 2\overrightarrow {MG} .(\overrightarrow {GA}  + \overrightarrow {GB}  + \overrightarrow {GC} )$
               $= 3M{G^2} + \frac{1}{3}({a^2} + {b^2} + {c^2})$
               $\geqslant \frac{1}{3}({a^2} + {b^2} + {c^2})$
Đẳng thức xảy ra khi và chì khi M trùng G
Vậy min T = $\frac{1}{3}({a^2} + {b^2} + {c^2})$ khi và chỉ khi M trùng G.

Phương pháp 3: Tìm cực trị nhờ đánh giá tích vô hướng của hai vector:
Ví dụ 3.1:
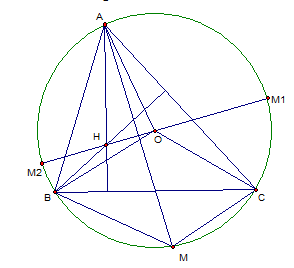
Cho tam giác ABC không đều nội tiếp đường tròn (O). Tìm trên đường tròn điểm M để có tổng bình phương khoảng cách từ đó đến ba đỉnh tam giác là nhò nhất, lớn nhất.
Giải:
Với mọi điểm M thuộc đường tròn (O) ta có:
                          
$T = M{A^2} + M{B^2} + M{C^2}$
     $= {(\overrightarrow {MO}  + \overrightarrow {OA} )^2} + {(\overrightarrow {MO}  + \overrightarrow {OB} )^2} + {(\overrightarrow {MO}  + \overrightarrow {OC} )^2}$
     $= 6{R^2} + 2\overrightarrow {MO} (\overrightarrow {OA}  + \overrightarrow {OB}  + \overrightarrow {OC} )$
     $= 6{R^2} + 2\overrightarrow {MO} .\overrightarrow {OH}$ ( với H là trực tâm của tam giác)
     $= 6{R^2} + 2R.OH.\cos \alpha (\alpha  = (\overrightarrow {MO} ,\overrightarrow {OH} ))$
Từ đó suy ra
T nhỏ nhất $\Leftrightarrow \cos \alpha  =  - 1 \Leftrightarrow \overrightarrow {MO}  \uparrow  \downarrow \overrightarrow {OH}$
T lớn nhất $\Leftrightarrow \cos \alpha  = 1 \Leftrightarrow \overrightarrow {MO}  \uparrow  \uparrow \overrightarrow {OH}$

Ví dụ 3.2:
Cho tam giác ABC vuông tại A. Gọi  là góc $\alpha$ giữa hai trung tuyến BD và CK. Tìm giá trị nhỏ nhất của cos$\alpha$
Giải:
Ta có
 $\cos \alpha  = |\frac{{\overrightarrow {BD} .\overrightarrow {CK} }}{{BD.CK}}|$
             $= \frac{{|(\overrightarrow {BA}  + \overrightarrow {BC} ).(\overrightarrow {CA}  + \overrightarrow {CB} )|}}{{4.BD.CK}}$
             $= \frac{{|\overrightarrow {BA} .\overrightarrow {CA}  + \overrightarrow {BC} (\overrightarrow {CA}  - \overrightarrow {BA} ) - {{\overrightarrow {BC} }^2}|}}{{4.BD.CK}}$                
             $= \frac{{B{C^2}}}{{2.BD.CK}}(doBA \bot CA)$
Mặt khác:
$2.BD.CK \leqslant B{D^2} + C{K^2} = \frac{1}{4}(2.A{B^2} + 2.B{C^2} - A{C^2}) + \frac{1}{4}(2A{C^2} + 2B{C^2} - A{B^2})$
                     $= \frac{{5B{C^2}}}{4}$ ( do $B{C^2} = A{B^2} + A{C^2}$)
Do đó   $\cos \alpha  \geqslant \frac{{B{C^2}}}{{\frac{{5B{C^2}}}{4}}} = \frac{4}{5}$
Đẳng thức xảy ra khi và chỉ khi BD = CK khi và chỉ khi tam giác ABC vuông cân tại đỉnh A
Vậy $\min \cos \alpha  = \frac{4}{5}$

Ví dụ 3.3:
Cho tam giác ABC. Tìm điểm M sao cho biểu thức sau đạt giá trị nhỏ nhất:
                      $T = 2.\cos \frac{A}{2}.MA + MB + MC$
 Giải:
Ta có:
 $T = 2.\cos \frac{A}{2}.MA + \frac{{MB.AB}}{{AB}} + \frac{{MC.AC}}{{AC}}$
    $\geqslant 2.\cos \frac{A}{2}.MA + \frac{{\overrightarrow {MB} .\overrightarrow {AB} }}{{AB}} + \frac{{\overrightarrow {MC} .\overrightarrow {AC} }}{{AC}}$
    $= 2.\cos \frac{A}{2} + \frac{{(\overrightarrow {MA}  + \overrightarrow {AB} ).\overrightarrow {AB} }}{{AB}} + \frac{{(\overrightarrow {MA}  + \overrightarrow {AC} ).\overrightarrow {AC} }}{{AC}}$
    $= 2\cos \frac{A}{2}.MA + \overrightarrow {MA} (\frac{{\overrightarrow {AB} }}{{AB}} + \frac{{\overrightarrow {AC} }}{{AC}}) + AB + AC$
Do đó ta có:
$2.\cos \frac{A}{2}.MA + MB + MC \geqslant 2\cos \frac{A}{2}.MA + \overrightarrow {MA} (\frac{{\overrightarrow {AB} }}{{AB}} + \frac{{\overrightarrow {AC} }}{{AC}}) + AB + AC(1)$
Mặt khác lại có:
${(\frac{{\overrightarrow {AB} }}{{AB}} + \frac{{\overrightarrow {AC} }}{{AC}})^2} = \frac{{A{B^2}}}{{A{B^2}}} + \frac{{A{C^2}}}{{A{C^2}}} + 2.\frac{{\overrightarrow {AB} }}{{AB}}.\frac{{\overrightarrow {AC} }}{{AC}}$
                       $= 1 + 1 + 2\cos A = 2(1 + \cos A) = 4{\cos ^2}\frac{A}{2}$
Suy ra: $|\frac{{\overrightarrow {AB} }}{{AB}} + \frac{{\overrightarrow {AC} }}{{AC}}| = 2|\cos \frac{A}{2}|$
Do đó :
$2\cos \frac{A}{2}.MA + \overrightarrow {MA} (\frac{{\overrightarrow {AB} }}{{AB}} + \frac{{\overrightarrow {AC} }}{{AC}}) = 2.MA\left[ {\cos \frac{A}{2}} \right. + |\cos \frac{A}{2}|\cos (\overrightarrow {MA} ,\overrightarrow u )] \geqslant 0(2)$
                                                                      (với $\overrightarrow u  = \frac{{\overrightarrow {AB} }}{{AB}} + \frac{{\overrightarrow {AC} }}{{AC}}$)
Vì vậy:
$2.\cos \frac{A}{2}.MA + MB + MC \geqslant AB + AC$
 Đẳng thức (1) xảy ra khi và chỉ khi $\overrightarrow {MB}  \uparrow  \uparrow \overrightarrow {AB}$  và  $\overrightarrow {MC}  \uparrow  \uparrow \overrightarrow {AC}$     
$\Leftrightarrow M \equiv A$ (thỏa mãn (2))
Vậy Min T= AB+AC khi và chì khi M trùng A

BÀI TẬP RÈN LUYỆN:
Bài 1:
Cho$\Delta ABC$ có $\hat A = {60^0}$. Tìm giá trị nhỏ nhất của biểu thức $T = \sqrt 3 MA + MB + MC$.
Hướng dẫn:
$T = \sqrt 3 MA + \frac{{MB.AB}}{{AB}} + \frac{{MC.AC}}{{AC}}$
    $\begin{array}    \geqslant \sqrt 3 MA + \frac{{\overrightarrow {MB} .\overrightarrow {AB} }}{{\overrightarrow {AB} }} + \frac{{\overrightarrow {MC} .\overrightarrow {AC} }}{{\overrightarrow {AC} }}  \\    = 2\cos \frac{A}{2}MA + \overrightarrow {MA} .\left( {\overrightarrow {\frac{{AB}}{{AB}}}  + \frac{{\overrightarrow {AC} }}{{AC}}} \right) + AB + AC.  \\ \end{array}$    
Bình phương tổng $\left( {\overrightarrow {\frac{{AB}}{{AB}}}  + \frac{{\overrightarrow {AC} }}{{AC}}} \right)$ ta có $\left| {\overrightarrow {\frac{{AB}}{{AB}}}  + \frac{{\overrightarrow {AC} }}{{AC}}} \right| = 2\left| {\cos \frac{A}{2}} \right|$ suy ra điều phải chứng minh.

Bài 2:
Cho$\Delta ABC$ ngoại tiếp đường tròn tâm I. Tìm giá trị lớn nhất của biểu thức
                                                    $T = \frac{{IA.IB.IC}}{{aI{A^2} + bI{B^2} + cI{C^2}}}$.     
Hướng dẫn:
Bình phương vô hướng ${\left( {a\overrightarrow {IA}  + b\overrightarrow {IB}  + c\overrightarrow {IC} } \right)^2} = 0$ suy ra $aI{A^2} + bI{B^2} + cI{C^2} = abc$.
Max T = $\frac{{\sqrt 3 }}{9} \Leftrightarrow$$\Delta ABC$ đều.                 

Bài 31:
Cho $\widehat {xOy}$ = $\alpha$ và một độ dài a. Trên hai cạnh Ox, Oy lần lượt lấy các điểm A, B sao cho OA + OB = a. Tìm độ dài ngắn nhất của đoạn AB.
Hướng dẫn:
 $\overrightarrow {AB}  = \overrightarrow {OB}  - \overrightarrow {OA}  \Rightarrow A{B^2} = O{B^2} + O{A^2} - 2\overrightarrow {OA} .\overrightarrow {OB}$
              $\begin{array}    = {\left( {OA + OB} \right)^2} - 2OA.OB - 2OA.OB.\cos \alpha   \\    = {a^2} - 2OA.OB\left( {1 + \cos \alpha } \right)  \\    \geqslant {a^2} - 2.{\left( {\frac{{OA + OB}}{2}} \right)^2}.\left( {1 + \cos \alpha } \right)  \\    = \frac{{{a^2}}}{4}\left( {2 - 2\cos \alpha } \right)  \\ \end{array}$
Dấu “=” xảy ra OA = OB = $\frac{a}{2}$.
Vậy min AB = $\frac{a}{2}\sqrt {2 - 2\cos \alpha }$.

Bài 3:
Từ điểm I trên cạnh BC của$\Delta ABC$ dựng $IN//AB$, $IM//AC$. Xác định vị trí điểm I sao cho MN có độ dài ngắn nhất.
Hướng dẫn:
Đặt $\frac{{IB}}{{BC}} = x$ thì $\frac{{IC}}{{BC}} = 1 - x\left( {0 < x < 1} \right).$
Ta có $\overrightarrow {AN}  = x\overrightarrow {AC} ,\overrightarrow {AM}  = \left( {1 - x} \right)\overrightarrow {AB}$ nên $\overrightarrow {MN}  = \overrightarrow {AN}  - \overrightarrow {AM}  = x\overrightarrow {AC}  - \left( {1 - x} \right)\overrightarrow {AB}  = x\overrightarrow {AD}  - \overrightarrow {AB}$(ABCD là hình bình hành).
Tìm điểm K trên cạnh AD để $\overrightarrow {AK}  = x\overrightarrow {AD}$ thì $\overrightarrow {MN}  = \overrightarrow {AK}  - \overrightarrow {AB}  = \overrightarrow {BK}$.
Vậy MN ngắn nhất$\Leftrightarrow$ BK ngắn nhất$\Leftrightarrow$$BK \bot AD$.
Từ đó ta suy ra cách dựng điểm I.

Bài 4:
Cho tứ giác lồi ABCD, M là điểm tùy ý trên cạnh CD. Gọi $P,{P_1},{P_2}$ lần lượt là chu vi các tam giác AMB, ACB, ADB. Cmr: $P < \max \left\{ {{P_1},} \right.\left. {{P_2}} \right\}$.
Hướng dẫn:
M thuộc cạnh CD nên $\overrightarrow {AM}  = \frac{{MD}}{{CD}}.\overrightarrow {AC}  + \frac{{MC}}{{CD}}.\overrightarrow {AD}$
            $\overrightarrow {BM}  = \frac{{MD}}{{CD}}.\overrightarrow {BC}  + \frac{{MC}}{{CD}}.\overrightarrow {BD}$
Do đó $AM = \left| {\frac{{MD}}{{CD}}.\overrightarrow {AC}  + \frac{{MC}}{{CD}}.\overrightarrow {AD} } \right| < \left| {\frac{{MD}}{{CD}}.\overrightarrow {AC} } \right| + \left| {\frac{{MC}}{{CD}}.\overrightarrow {AD} } \right| = \frac{{MD}}{{CD}}.AC + \frac{{MC}}{{CD}}.AD$(Dấu “=” không xảy ra vì $\frac{{MD}}{{CD}}.\overrightarrow {AC} ,\frac{{MC}}{{CD}}.\overrightarrow {AD}$ không cùng phương).
Tương tự với BM.
Suy ra $AM + BM < \frac{{MD}}{{CD}}\left( {AC + BC} \right) + \frac{{MC}}{{CD}}\left( {AD + BD} \right)$
        $\leqslant \left( {\frac{{MD}}{{CD}} + \frac{{MC}}{{CD}}} \right).\max \left\{ {AC + BC,AD + \left. {BD} \right\}.} \right.$
Như vậy AM + BM < $\max \left\{ {AC + BC,AD + \left. {BD} \right\},} \right.$suy ra
AM + BM + AB < $\max \left\{ {AC + BC + AB,AD + \left. {BD + AB} \right\}} \right.$(đpcm)

Bài 5:
Cho M là một điểm thuộc miền trong$\Delta ABC$. Gọi H, I, K theo thứ tự là hình chiếu của M trên BC, CA, AB. Tìm vị trí của M để $M{H^2} + M{I^2} + M{K^2}$ đạt giá trị nhỏ nhất.
Hướng dẫn:
Áp dụng bất đẳng thức Bunhiacốpxki:
$\begin{array}   {\left( {aMH + bMI + cMK} \right)^2} \leqslant \left( {{a^2} + {b^2} + {c^2}} \right)\left( {M{H^2} + M{I^2} + M{K^2}} \right)  \\    \Rightarrow M{H^2} + M{I^2} + M{K^2} \geqslant \frac{{4{S^2}_{ABC}}}{{{a^2} + {b^2} + {c^2}}}.  \\ \end{array}$
Dấu “=” xảy ra $\Leftrightarrow \frac{{MH}}{a} = \frac{{MI}}{b} = \frac{{MK}}{c}$
         $\Leftrightarrow \frac{{{S_{MBC}}}}{{{a^2}}} = \frac{{{S_{MCA}}}}{{{b^2}}} = \frac{{{S_{MAB}}}}{{{c^2}}}$    
                  $\Leftrightarrow {a^2}\overrightarrow {MA}  + {b^2}\overrightarrow {MB}  + {c^2}\overrightarrow {MC}  = 0$
         $\Leftrightarrow$M là điểm Lemoine của $\Delta ABC$.    

Bài 6:
Cho$\Delta ABC$ và một điểm M tùy ý. Tìm giá trị nhỏ nhất của tồng
$T = {a^2}M{A^2} + {b^2}M{B^2} + {c^2}M{C^2}$.
Hướng dẫn:
Ta có ${a^2}\overrightarrow {MA}  + {b^2}\overrightarrow {MB}  + {c^2}\overrightarrow {MC}  \geqslant 0$ nên
${a^4}M{A^2} + {b^4}M{B^2} + {c^4}M{C^2} + 2{a^2}{b^2}\overrightarrow {MA} .\overrightarrow {MB}  + 2{b^2}{c^2}\overrightarrow {MB} .\overrightarrow {MC}  + 2{a^2}{c^2}\overrightarrow {MA} .\overrightarrow {MC}  \geqslant 0$
Chú ý: $2\overrightarrow {MX} .\overrightarrow {MY}  = M{X^2} + M{Y^2} - X{Y^2},\forall X,Y$ta có:
$T = {a^2}M{A^2} + {b^2}M{B^2} + {c^2}M{C^2} \geqslant \frac{{3{a^2}{b^2}{c^2}}}{{{a^2} + {b^2} + {c^2}}}.$
Dấu “=” xảy ra $\Leftrightarrow {a^2}\overrightarrow {MA}  + {b^2}\overrightarrow {MB}  + {c^2}\overrightarrow {MC}  = \overrightarrow 0  \Leftrightarrow$M là điểm Lemoine của $\Delta ABC$