|
|
1. Hệ hai phương trình bậc nhất hai ẩn
Cho hai phương trình bậc nhất hai ẩn $ax + by = c$ và $ a'x + b'y = c'$ (tức là ${a^2} + {b^2} \ne 0\,\,,a{'^2} + b{'^2} \ne 0\,$). Khi đó, ta có hệ hai phương trình bậc nhất hai ẩn sau:
$(I)\left\{ \begin{gathered}
{\text{ax}} + by = c \\
a'x + b'x = c' \\
\end{gathered} \right.$
Mỗi cặp số $({x_0};{y_0})$đồng thời là nghiệm của cả hai phương trình trong hệ được gọi là một nghiệm của hệ.
Giải hệ phương trình là tìm tất cả các nghiệm của nó.
Các khái niệm hệ phương trình tương đương, hệ phương trình hệ quả cũng tương tự như đối với phương trình.
Đối với hệ phương trình, chúng ta cũng có những phép biến đổi tương đương, tức là phép biến đổi một hệ phương trình thành một hệ phương trình khác tương đương với nó. Biến đổi hệ phương trình bằng cách áp dụng quy tắc cộng đại số hoặc quy tắc thế mà ta đã học chính là những phép biến đổi tương đương các hệ phương trình.
Giả sử (d) là đường thẳng $ax + by = c$ và (d’) là đường thẳng $a'x + b'y = c'$. Khi đó:
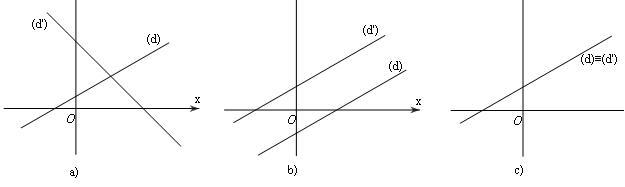
1) Hệ (I) có nghiệm duy nhất $ \Leftrightarrow $(d) và (d’) cắt nhau;
2) Hệ (I) vô nghiệm$ \Leftrightarrow $(d) và (d’) song song với nhau;
3) Hệ (I) có vô số nghiệm $ \Leftrightarrow $ (d) và (d’) trùng nhau.
2. Giải và biện luận hệ hai phương trình bậc nhất hai ẩn.
a, Xây dựng công thức
Xét hệ phương trình bậc nhất hai ẩn
(I) $\left\{ \begin{gathered}
{\text{ax}} + by = c\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,(1) \\
a'x + b'y = c'\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,(2) \\
\end{gathered} \right.$
- Nhân hai vế của phương trình (1) với b’, hai vế của phương trình (2) với –b rồi cộng các vế tương ứng, ta được
$(ab' - a'b)x = cb' - c'b$ (3)
- Nhân hai vế của phương trình (1) với –a’, hai vế của phương trình (2) với a rồi cộng các vế tương ứng, ta được
$(ab' - a'b)y = ac' - a'c$ (4)
- Trong (3) và (4) ta đặt $D = ab' - a'b,\,\,{D_x} = cb' - c'b\,,\,{D_y} = ac' - a'c$. Khi đó, ta có hệ phương trình hệ quả
(II)$\left\{ \begin{gathered}
D.\,x = {D_x} \\
D.y = {D_y} \\
\end{gathered} \right.$
Đối với hệ (II), ta xét các trường hợp sau:
1) $D \ne 0$: Hệ có một nghiệm duy nhất (x; y), trong đó
$x = \frac{{{D_x}}}{D};\,\,y = \frac{{{D_y}}}{D}$
2) $D = 0$
${D_x} \ne 0$hoặc${D_y} \ne 0$: Hệ vô nghiệm
${D_x} = {D_y} = 0$: Hệ có vô số nghiệm, tập nghiệm của hệ là tập nghiệm của phương trình $ax + by = c$
b, Thực hành giải và biện luận
Trong thực hành giải và biện luận hệ phương trình bậc nhất hai ẩn ,định thức là một công cụ đem lại nhiều thuận tiện.
Biểu thức $pq' - p'q $ với p, q, p’, q’ là những số, được gọi là một định thức cấp 2 và kí hiệu là
$\left| \begin{gathered}
p\,\,\,\,\,\,\,\,\,q \\
p'\,\,\,\,\,\,\,\,q' \\
\end{gathered} \right|\,\,$
Như vậy, các biểu thức $D;{D_x};{D_y}$mà chúng ta gặp khi giải hệ (I) đều là những định thức cấp hai:
$D = ab' - a'b = \left| \begin{gathered}
a\,\,\,\,\,\,\,\,\,b \\
a'\,\,\,\,\,\,\,\,b' \\
\end{gathered} \right|,\,\,{D_x} = cb' - c'b = \left| \begin{gathered}
c\,\,\,\,\,\,\,\,\,b \\
c'\,\,\,\,\,\,\,\,b' \\
\end{gathered} \right|,\,{D_y} = ac' - a'c = \left| \begin{gathered}
a\,\,\,\,\,\,\,\,\,c \\
a'\,\,\,\,\,\,\,\,c' \\
\end{gathered} \right|$
Ta thấy trong mỗi định thức trên đều có hai hàng và hai cột
Ta có thể sử dụng định thức để giải hệ phương trình bậc nhất hai ẩn.
Ví dụ 2: Giải và biện luận hệ phương trình
$\left\{ \begin{gathered}
mx + y = m + 1 \\
x + my = 2 \\
\end{gathered} \right.$
Giải
Trước hết, ta tính các định thức
$D = \left| \begin{gathered}
m\,\,\,\,\,\,\,\,\,\,1 \\
1\,\,\,\,\,\,\,\,\,\,\,\,m \\
\end{gathered} \right| = {m^2} - 1 = (m - 1)(m + 1)$
${D_x} = \left| \begin{gathered}
m\, + 1\,\,\,\,\,\,\,\,\,\,\,1 \\
2\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,m \\
\end{gathered} \right| = {m^2} + m - 2 = (m - 1)(m + 2)$
${D_y} = \left| \begin{gathered}
m\,\,\,\,\,\,\,\,m + 1 \\
1\,\,\,\,\,\,\,\,\,\,\,\,\,\,2 \\
\end{gathered} \right| = {m^{}} - 1$
Ta phải xét các trường hợp sau:
1)$D \ne 0$, tức là $m \ne \pm 1$. Ta có:
$x = \frac{{{D_x}}}{D} = \frac{{(m - 1)(m + 2)}}{{\left( {m - 1} \right)\left( {m + 1} \right)}} = \frac{{m + 2}}{{m + 1}}$
$y = \frac{{{D_y}}}{D} = \frac{{m - 1}}{{\left( {m - 1} \right)\left( {m + 1} \right)}} = \frac{1}{{m + 1}}$
Hệ có một nghiệm duy nhất $\left( {x;y} \right) = \left( {\frac{{m + 2}}{{m + 1}};\frac{1}{{m + 1}}} \right)$
2)$D = 0$, tức là m = 1 hoặc m = -1
- Nếu m = 1 thì $D = {D_x} = {D_y} = 0$và hệ trở thành $\left\{ \begin{gathered}
x + y = 2 \\
x + y = 2 \\
\end{gathered} \right.$. Ta có
$\left\{ \begin{gathered}
x + y = 2 \\
x + y = 2 \\
\end{gathered} \right. \Leftrightarrow x + y = 2 \Leftrightarrow \left\{ \begin{gathered}
x \in \mathbb{R} \\
y = 2 - x \\
\end{gathered} \right.$
- Nếu m= -1 thì $D = 0$, nhưng ${D_x} \ne 0$nên hệ vô nghiệm
Kết luận
Với $m \ne \pm 1$, hệ có nghiệm duy nhất $\left( {x;y} \right) = \left( {\frac{{m + 2}}{{m + 1}};\frac{1}{{m + 1}}} \right)$
Với m = -1, hệ vô nghiệm;
Với m = 1, hệ có vô số nghiệm (x; y) tính theo công thức
$\left\{ \begin{gathered}
x \in \mathbb{R} \\
y = 2 - x \\
\end{gathered} \right.$
3. Ví dụ về giải hệ phương trình bậc nhất ba ẩn
Hệ phương trình bậc nhất ba ẩn có dạng tổng quát là
$\left\{ \begin{gathered}
{a_1}x + {b_1}y + {c_1}z = {d_1} \\
{a_2}x + {b_2}y + {c_2}z = {d_2} \\
{a_3}x + {b_3}y + {c_3}z = {d_3} \\
\end{gathered} \right.$
Trong đó các hệ số của ba ẩn x, y, z trong mỗi phương trình của hệ không đồng thời bẳng 0.
Giải hệ phương trình trên là tìm tất cả các bộ ba số (x; y; z) đồng thời nghiệm đúng cả ba phương trình của hệ.
NHẬN XÉT
Nguyên tắc chung để giải các hệ phương trình nhiều ẩn là khử bớt ẩn để quy về giải các phương trình hay hệ phương trình có số ẩn ít hơn. Để khử bớt ẩn, ta cũng có thể dùng các phương pháp cộng đại số hay phương pháp thế giống như đối với hệ phương trình hai ẩn.
|