|
|
1.Đường tiệm cận đứng và đường tiệm cận ngang
ĐỊNH NGHĨA 1
Đường thẳng $y = {y_0}$ được gọi là đường tiệm cận ngang (gọi tắt là tiệm cận ngang) của đồ thị hàm số $y = f(x)$. nếu $\mathop {\lim }\limits_{x \to + \infty } f(x) = {y_0}$ hoặc $\mathop {\lim }\limits_{x \to - \infty } f(x) = {y_0}$
ĐỊNH NGHĨA 2
Đường thẳng $x = {x_0}$ được gọi là đường tiệm cận đứng (gọi tắt là tiệm cận đứng) của đồ thị hàm số $y = f(x)$ nếu ít nhất một trong các điêù kiện sau được thoả mãn $\begin{gathered}
\mathop {\lim }\limits_{x \to x_0^ - } f(x) = + \infty ;\,\,\,\mathop {\lim }\limits_{x \to x_0^ + } f(x) = + \infty ; \\
\mathop {\lim }\limits_{x \to x_0^ - } f(x) = - \infty ;\mathop {\lim }\limits_{x \to x_0^ + } f(x) = - \infty ; \\
\end{gathered} $
VÍ DỤ
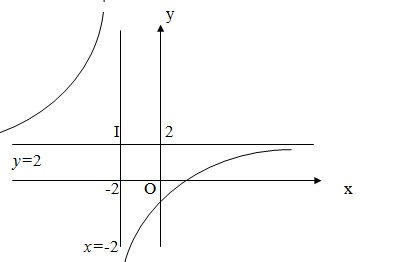
Tìm tiệm cận ngang và tiệm cận đứng của đồ thi hàm số$y = \frac{{2x - 1}}{{x + 2}}$
Giải
Hàm số đã cho có tập hợp xác định $\mathbb{R}\backslash \left\{ { - 2} \right\}$
Vì $\mathop {\lim y=2}\limits_{x \to +\infty }$ và $\mathop {\lim y=2}\limits_{x \to -\infty }$ nên đường thẳng $y=2$ là tiệm cận ngang của đồ thị (khi $x \rightarrow + \infty $ và khi $x \rightarrow - \infty $)
Vì $\mathop {\lim y=- \infty }\limits_{x \to (-2)^{+} }$ và $\mathop {\lim
y=+ \infty }\limits_{x \to (-2)^{-} }$ nên đường thẳng $y=2$ là tiệm cận đứng của đồ thị (khi $x \rightarrow (-2)^{-} $ và khi $x \rightarrow (-2)^{+} $)
2. Đường tiệm cận xiên
ĐỊNH NGHĨA 3
Đường thẳng $y = {\text{ax}} + b\,\,(a \ne 0)$ được gọi là đường tiệm cận xiên ( gọi tắt tiệm cận xiên) của đồ thị hàm số $y = f(x)$ nếu
$\mathop {\lim }\limits_{x \to + \infty } y = \left[ {f(x) - ({\text{ax}} + b)} \right] = 0$
hoặc $\mathop {\lim }\limits_{x \to - \infty } y = \left[ {f(x) - ({\text{ax}} + b)} \right] = 0$
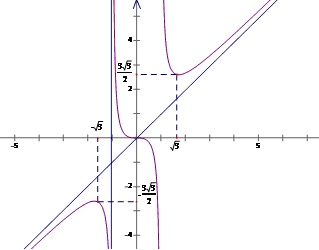
Ví dụ: Đồ thị hàm số $f(x) = x + \frac{x}{{{x^2} - 1}}$ có tiệm cận xiên ( khi $x \to + \infty \,\& \,x \to - \infty $) là đường thẳng y=x vì $\mathop {\lim }\limits_{x \to + \infty } \frac{x}{{{x^2} - 1}} = 0\,\,\,\& \,\,\,\mathop {\lim }\limits_{x \to - \infty } \left[ {f(x) - x} \right] = 0$
CHÚ Ý
Để xác định các hệ số a,b trong phương trình của đường tiệm cận xiên, ta có thể áp dụng các công thức sau:
$a = \mathop {\lim }\limits_{x \to + \infty } \frac{{f(x)}}{x};\,\,\,\,\,\,b = \mathop {\lim }\limits_{x \to + \infty } \left[ {f(x) - ax} \right]$
Hoặc $a = \mathop {\lim }\limits_{x \to - \infty } \frac{{f(x)}}{x};\,\,\,\,\,\,b = \mathop {\lim }\limits_{x \to - \infty } \left[ {f(x) - ax} \right]$
(khi $a = 0$ thì ta có tiệm cận ngang)
|