|
|
1.Trục toạ độ
Trục toạ độ (còn gọi là trục hay trục số) là một đường thẳng trên đó đã xác định điểm O và một vectơ $\overrightarrow i $ có độ dài bằng l.
 (Hình 27 trang 25) (Hình 27 trang 25)
Điểm O gọi là gốc toạ độ, vectơ $\overrightarrow i $ gọi là vectơ đơn vị của trục toạ độ
Trục tọa độ như vậy được kí hiệu là $(O;\overrightarrow i )$
Toạ độ của vectơ và của điểm trên trục
Cho vectơ $\overrightarrow u $ nằm trên trục $\left( {O;\,\overrightarrow i } \right)$. Khi đó có số a xác định để $\overrightarrow u = a\overrightarrow i $. Số a như thế gọi là tọa độ của vectơ $\overrightarrow u $ đối với trục $\left( {O;\,\overrightarrow i } \right)$.
Cho điểm $M$ nằm trên trục $\left( {O;\,\overrightarrow i } \right)$. Khi đó số m xác định để $\overrightarrow {OM} = m\overrightarrow i $.Số m như thế gọi là tọa độ của điểm M đối với trục $\left( {O;\,\overrightarrow i } \right)$ ( cũng là tọa độ của vecto $\overrightarrow {OM} $
Độ dài đại số của vectơ trên trục
Nếu hai điểm A, B nằm trên trục Ox thì tọa độ của vectơ $\overrightarrow {AB} $ được kí hiệu là $\overline {AB} $và gọi là độ dài đại số của vectơ $\overrightarrow {AB} $ trên trục Ox.
Như vậy
$\overrightarrow {AB} = \overline {AB} \,\,\overrightarrow i $
2. Hệ trục toạ độ
Trên hình vẽ ta có 1 hệ trục tọa độ vuông góc. Nó bao gồm 2 trục tọa độ $Ox$ và $Oy$ vuông góc với nhau. Vecto đơn vị trên trục $Ox$ là $\overrightarrow i $, vecto đơn vị trên trục $Oy$ là $\overrightarrow j $
Điểm $O$ gọi là gốc toạ độ. Trục $Ox$ gọi là trục hoành, trục $Oy$ gọi là trục tung.
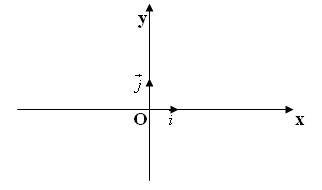
Hệ trục toạ độ vuông góc như trên còn gọi đơn giản là hệ trục toạ độ và kí hiệu là $Oxy$ hay $\left( {O;\overrightarrow i ;\overrightarrow j } \right)$.
CHÚ Ý
Khi trong mặt phẳng đã cho(hay đã chọn) một hệ trục toạ độ ,ta sẽ goi đó là mặt phẳng toạ độ
3. Toạ độ của vectơ đối với hệ trục toạ độ
Đinh nghĩa
Đối với hệ trục toạ độ $\left( {O;\overrightarrow i ;\overrightarrow j } \right)$, nếu $\overrightarrow a = x\overrightarrow i + y\overrightarrow j $ thì cặp số (x; y) được gọi là toạ độ của vectơ $\overrightarrow a $, kí hiệu là $\overrightarrow a = \left( {x;y} \right)$hay $\overrightarrow a \left( {x;y} \right)$. Số thứ nhất x gọi là hoành độ ,số thứ hai y goi là tung độ vủa vectơ$\overrightarrow a $.
Nhận xét: Từ định nghĩa toạ độ vectơ ta thấy hai vectơ bằng nhau khi và chỉ khi có cùng toạ độ nghĩa là
$\overrightarrow a (x;y) = \overrightarrow b (x';y') \Leftrightarrow \left\{ \begin{gathered}
x = x' \\
y = y' \\
\end{gathered} \right.$
4. Bỉểu thưc toạ độ của các phép toán vectơ
Một cách tổng quát ta có
Cho $\overrightarrow a = \left( {x;y} \right)$ và $\overrightarrow b = \left( {x';y'} \right)$. Khi đó
1) $\overrightarrow a + \overrightarrow b = (x + x';y + y');\overrightarrow a - \overrightarrow b = (x - x';y - y')$
2) $k\overrightarrow a = (kx;ky)$với $k \in \mathbb{R}$
3) Vec tơ $\overrightarrow b $cùng phương với vectơ $\overrightarrow a \ne \overrightarrow 0 $ khi và chỉ khi có số k sao cho $x' = kx,\,\,y' = ky$.
5. Toạ độ của điểm
Trong măt phẳng toạ độ $Oxy$, tọa độ của vectơ $\overrightarrow {OM} $ được gọi là toạ độ của điểm $M$
Tổng quát
Vơi hai điểm $M\left( {{x_M};{y_M}} \right),\,\,N\left( {{x_N};{y_N}} \right)$
$\overrightarrow {MN} = ({x_N} - {x_M};\,{y_N} - {y_M})$
CHÚ Ý:
Để thuận tiện, ta thường dùng kí hiệu $\left( {{x_M};{y_M}} \right)$ để chỉ tọa độ của điểm $M$.
6. Toạ độ trung điểm của đoạn thẳng và toạ độ của trọng tâm tam giác
Nếu $P$ là trung điểm của đoạn thẳng $MN$ thì
${x_p} = \frac{{{x_M} + {x_N}}}{2};\,\,\,{y_p} = \frac{{{y_M} + {y_N}}}{2}$
Nếu $G$ là trọng tâm của tam giác $ABC$ thì
${x_G} = \frac{{{x_A} + {x_B} + {x_C}}}{3};\,\,\,{y_G} = \frac{{{y_A} + {y_B} + {y_C}}}{3}$
Ví dụ: Trong mặt phẳng toạ độ $Oxy$ ,cho các điểm $A(2:0), B(0:4),C(1:3)$
a) Chứng minh $A,B,C$ là ba đỉnh của tam giác
b) Tìm toạ độ của trọng tâm tam giác $ABC$
Giải:
a) Ta có$\overrightarrow {AB} = ( - 2;\,4)\,$và $\overrightarrow {AC} = ( - 1;3)\,$. Do $\frac{{ - 2}}{{ - 1}} \ne \frac{4}{3}$nên $\overrightarrow {AB} ,\,\,\overrightarrow {AC} $ không cùng một phương, suy ra A, B, C không thẳng hàng và chúng là ba đỉnh của một tam giác.
b) Ta có $\frac{{{x_A} + {x_B} + {x_C}}}{3} = \frac{{2 + 0 + 1}}{3} = 1$ và $\frac{{{y_A} + {y_B} + {y_C}}}{3} = \frac{{0 + 4 + 3}}{3} = \frac{7}{3}$
Vậy tọa độ của trọng tâm tam giác ABC là $\left( {1;\frac{7}{3}} \right)$
|