|
|
1. Hệ trục tọa độ trong không gian
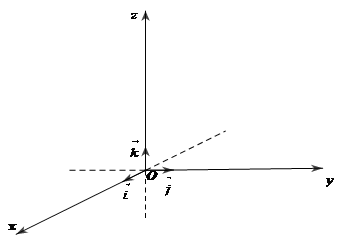
- Định nghĩa: Hệ gồm $3$ trục $Ox, Oy, Oz$ đôi một vuông góc được gọi là hệ trục tọa độ vuông góc trong không gian
Thuật ngữ và ký hiệu:
- Hệ trục tọa độ trong định nghĩa trên còn được gọi đơn giản là hệ tọa độ trong không gian, ký hiệu là $Oxyz$. Ta thường gọi các vecto đơn vị trên các trục $Ox, Oy, Oz$ lần lượt là $\overrightarrow {i,} \,\overrightarrow {j,} \,\overrightarrow k $ và còn ký hiệu hệ trục tọa độ là $(O;\overrightarrow {i,} \,\overrightarrow {j,} \,\overrightarrow k )$. Điểm $O$ gọi lả gốc của hệ tọa độ, $Ox$ gọi là trục hoành, $Oy $ là trục tung và $Oz$ là trục cao
- Các mặt phẳng đi qua 2 trong 3 trục tọa độ gọi là các mặt phẳng tọa độ, ta ký hiệu chúng là mp$(Oxy)$, mp$(Oyz)$ và mp$(Ozx)$ hoặc đơn giản hơn là $(Oxy), (Oyz), (Ozx)$
- Khi không gian đã có 1 hệ tọa độ $Oxyz$ thì nó được gọi là không gian tọa độ $Oxyz$ hoặc đơn giản hơn là không gian $Oxyz$
- Chú ý các đẳng thức sau:
$\begin{gathered}
{\overrightarrow i ^2} = {\overrightarrow j ^2} = {\overrightarrow k ^2} = 1 \\
\overrightarrow i .\overrightarrow j = \overrightarrow j .\overrightarrow k = \overrightarrow k .\overrightarrow i = 0 \\
\end{gathered} $
2. Tọa độ của vecto
- Trong không gian tọa độ $Oxyz$ với các vecto đơn vị $\overrightarrow i ,\overrightarrow j ,\overrightarrow k $ trên các trục, cho 1 vecto $\overrightarrow u $. Khi đó có bộ 3 số duy nhất (x;y;z) sao cho $\overrightarrow u = x\overrightarrow i + y\overrightarrow j + z\overrightarrow k $. Bộ 3 số đó gọi là tọa độ của vecto $\overrightarrow u $ đối với hệ tọa độ Oxyz và ký hiệu hoặc $\overrightarrow u (x;y;z)$
Vậy:$\overrightarrow u = (x;y;z) \Leftrightarrow \overrightarrow u (x;y;z) \Leftrightarrow \overrightarrow u = x\overrightarrow i + y\overrightarrow j + z\overrightarrow k $
Hiển nhiên ta có: $\overrightarrow i = (1;0;0)\,\,;\overrightarrow j = (0;1;1)\,\,;\overrightarrow k = (0;0;1)$
Từ định nghĩa về tọa độ của vecto, ta dễ dàng suy ra các tính chất sau:
Cho các vecto $\overrightarrow {{u_1}} = ({x_1};{y_1};{z_1}),\overrightarrow {{u_2}} = ({x_2};{y_2};{z_2}),\overrightarrow {{u_3}} = ({x_3};{y_3};{z_3})$ và số k tùy ý, ta có
$\begin{gathered}
1)\,\overrightarrow {{u_1}} = \overrightarrow {{u_2}} \Leftrightarrow {x_1} = {x_2},{y_1} = {y_2},{z_1} = {z_2} \\
2)\,\overrightarrow {{u_1}} \pm \overrightarrow {{u_2}} = ({x_1} \pm {x_2};{y_1} \pm {y_2};{z_1} \pm {z_2}) \\
3)\,k\overrightarrow {{u_1}} = (k{x_1};k{x_2};k{x_3}) \\
4)\,\overrightarrow {{u_1}} .\overrightarrow {{u_2}} = {x_1}{x_2} + {y_1}{y_2} + {z_1}{z_2} \\
5)\left| {\overrightarrow {{u_1}} } \right| = \sqrt {{{\overrightarrow {{u_1}} }^2}} = \sqrt {{x_1}^2 + {y_1}^2 + {z_1}^2} \\
6)\,\cos (\overrightarrow {{u_1}} ,\overrightarrow {{u_2}} ) = \frac{{{x_1}{x_2} + {y_1}{y_2} + {z_1}{z_2}}}{{\sqrt {{x_1}^2 + {y_1}^2 + {z_1}^2} .\sqrt {{x_2}^2 + {y_2}^2 + {z_2}^2} }}\,\,\,\,\,(\overrightarrow {{u_1}} \ne 0,\overrightarrow {{u_2}} \ne 0) \\
7)\,\overrightarrow {{u_1}} \bot \overrightarrow {{u_2}} \Leftrightarrow \overrightarrow {{u_1}} .\overrightarrow {{u_2}} = 0 \Leftrightarrow {x_1}{x_2} + {y_1}{y_2} + {z_1}{z_2}=0 \\
\end{gathered} $
3. Tọa độ của điểm
Trong không gian tọa độ $Oxyz$, mỗi điểm $M$ được hoàn toàn xác định bởi vecto $\overrightarrow {OM} $. Bởi vậy, nếu $(x;y;z)$ là tọa độ của $\overrightarrow {OM} $ thì ta cũng nói $(x;y;z)$ là tọa độ của điểm $M$ và ký hiệu là $M = (x;y;z)$ hoặc $M(x;y;z)$
Như vậy: $M = (x;y;z) \Leftrightarrow \overrightarrow {OM} = x\overrightarrow i + y\overrightarrow j + z\overrightarrow k $
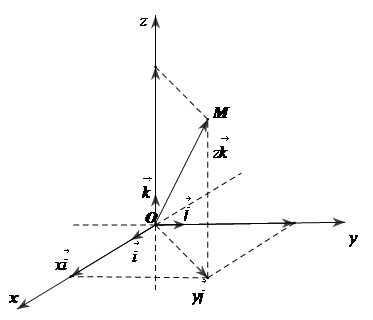
Số x gọi là hoành độ, y là tung độ và z là cao độ của điểm M
4. Liên hệ giữa tọa độ của vecto và tọa độ của 2 điểm mút
Cho 2 điểm $A({x_A};{y_A};{z_A})\& B({x_B};{y_B};{z_B})$. Khi đó ta có:
$\begin{gathered}
1)\,\overrightarrow {AB} = ({x_B} - {x_A};{y_B} - {y_A};{z_B} - {z_A}) \\
2)\,AB = \sqrt {{{({x_B} - {x_A})}^2} + {{({y_B} - {y_A})}^2} + {{({z_B} - {z_A})}^2}} \\
\end{gathered} $
5. Tích có hướng của 2 vecto:
Tích có hướng (hay tích vecto) của 2 vecto $\overrightarrow u (a;b;c)\& \overrightarrow v (a';b';c')$ là 1 vecto, kí hiệu là ${\text{[}}\overrightarrow u ,\overrightarrow v {\text{]}}$ hoặc $\overrightarrow u \wedge \overrightarrow v $, được xác định bằng tọa độ như sau:
${\text{[}}\overrightarrow u ,\overrightarrow v {\text{] = }}\left( {\left| \begin{gathered}
b\,\,\,\,\,c \\
b'\,\,\,c' \\
\end{gathered} \right|;\left| \begin{gathered}
c\,\,\,\,a \\
c'\,\,a' \\
\end{gathered} \right|;\left| \begin{gathered}
a\,\,\,\,b \\
a'\,\,b' \\
\end{gathered} \right|} \right) = \left( {bc' - b'c;ca' - a'c;ab' - a'b} \right)$
Tính chất của tích có hướng:
1. Vecto ${\text{[}}\overrightarrow u ,\overrightarrow v {\text{]}}$ vuông góc với cả 2 vecto $\overrightarrow u \& \overrightarrow v $ tức là:
${\text{[}}\overrightarrow u ,\overrightarrow v {\text{]}}{\text{.}}\overrightarrow u = {\text{[}}\overrightarrow u ,\overrightarrow v {\text{]}}.\overrightarrow v = 0$
2. $\left| {\left[ {\overrightarrow u ,\overrightarrow v } \right]} \right| = \left| {\overrightarrow u } \right|.\left| {\overrightarrow v } \right|.\sin (\overrightarrow u ,\overrightarrow v )$
3. $\left[ {\overrightarrow u ,\overrightarrow v } \right] = 0$ khi và chỉ khi 2 vecto $\overrightarrow u \& \overrightarrow v $ cùng phương
Ứng dụng của tích có hướng:
a) Tính diện tích hình bình hành:
Nếu ABCD là hình bình hành thì diện tích của nó là: $S = \left| {\left[ {\overrightarrow {AB} ,\overrightarrow {AD} } \right]} \right|$
b) Tính thể tích khối chóp:
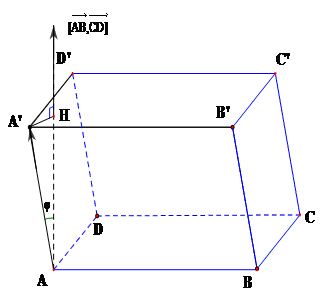
Nếu ABCD.A’B’C’D’ là hình hộp với diện tích đáy ABCD là S, chiều cao là h = AH, $\varphi $ là góc hợp bởi 2 vecto $\overrightarrow {{\text{AA}}'} \& \left[ {\overrightarrow {AB} ,\overrightarrow {AD} } \right]$ thì thể tích của hình hộp đó là:
$V = S.h = \left| {\left[ {\overrightarrow {AB} ,\overrightarrow {AD} } \right]} \right|.AH = \left[ {\overrightarrow {AB} ,\overrightarrow {AD} } \right].\left| {\overrightarrow {{\text{AA}}'} } \right|.c{\text{os}}\varphi $
Một số tính chất liên quan đến tích vô hướng và tích có hướng:
$\overrightarrow u \bot \overrightarrow v \Leftrightarrow \overrightarrow u .\overrightarrow v = 0$
$\overrightarrow u $ và $\overrightarrow v $ cùng phương $ \Leftrightarrow \left[ {\overrightarrow u ,\overrightarrow v } \right] = 0$
$\overrightarrow u ,\overrightarrow v ,\overrightarrow {\text{w}} $ đồng phẳng $ \Leftrightarrow \left[ {\overrightarrow u ,\overrightarrow v } \right].\overrightarrow {\text{w}} = 0$
6. Phương trình mặt cầu:
Trong không gian tọa độ Oxyz , mặt cầu tâm $I({x_0};{y_0};{z_0})$, bán kính R có phương trình:
${(x - {x_0})^2} + {(y - {y_0})^2} + {(z - {z_0})^2} = {R^2}$
Phương trình ${x^2} + {y^2} + {z^2} + 2ax + 2by + 2cz + d = 0$ là phương trình của mặt cầu khi và chỉ khi ${a^2} + {b^2} + {c^2} > d$. Khi đó tâm mặt cầu là điểm $I( - a; - b; - c)$ và bán kính: $R = \sqrt {{a^2} + {b^2} + {c^2} - d} $
|