|
|
1.Định nghĩa đường parabol
Cho một điểm F cố định và một đường thẳng $\Delta $cố định không đi qua F .Tập hợp các điểm M cách đều F và $\Delta $được gọi là đường parabol
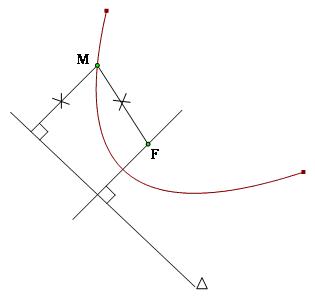
Điểm F gọi là tiêu điểm của parabol, đường thẳng $\Delta $ được gọi là đường chuẩn của parabol , khoảng cách từ F đến $\Delta $được gọi là tham số tiêu của parabol
2. Phương trình chính tắc của parabol
Ta có biểu thức (trang 111)
${y^2} = 2px\,\,\,\,\,\,\,\,(p > 0)$ (1)
Phương trình (1) gọi là phương trình chính tắc của parrabol
Ví dụ:
Viết phương trình chính tắc của parabol đi qua điểm M(2;5)
Giải : Phương trình chính tắc của parabol có dạng ${y^2} = 2px$. Thay tọa độ của M vào phương trình ta được 25 = 2.p.2, suy ra $p = \frac{{25}}{4}$. Từ đó ta được phương trình chính tắc của parabol đã cho là ${y^2} = \frac{{25}}{2}x$.
CHÚ Ý
Ở môn đại số , chúng ta gọi đồ thị của hàm số bậc hai $y = a{x^2} + bx + c$ là một đường parabol
Sở dĩ ta gọi vậy là thoả mãn định nghĩa của đương parabol mà ta vừa trình bày ở trên
|