|
|
1.Đường chuẩn của elip
Cho elip có phương trình chính tắc $\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} = 1\,\,\,\,\,\,(a > b > 0)$. Khi đó đường thẳng ${\Delta _1}:x + \frac{a}{e} = 0$ gọi là đường chuẩn của elip, ứng với tiêu điểm F1( -c ; 0)
Đường thẳng ${\Delta _2}:x - \frac{a}{e} = 0$ gọi là đường chuẩn của elip, ứng với tiêu điểm.

Tính chất
Với mọi điểm M của elip, ta luôn có:
$\frac{{M{F_1}}}{{d(M;{\Delta _1})}} = \frac{{M{F_2}}}{{d(M;{\Delta _2})}} = e\,\,\,\,\,\,\,\,(e < 1)$
2.Đường chuẩn của hypepol
Ta cũng định nghĩa đường chuẩn của hypebol tương tự như đối với elip
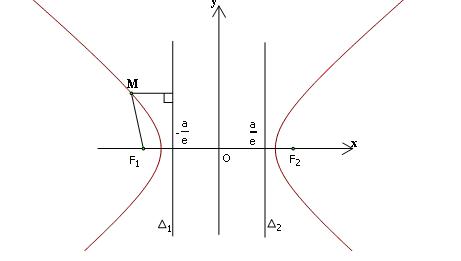
Ta cũng dễ dàng chứng minh được tính chất sau
Với mọi điểm M nằm trên (H), ta luôn có:
$\frac{{M{F_1}}}{{d(M;{\Delta _1})}} = \frac{{M{F_2}}}{{d(M;{\Delta _2})}} = e\,\,\,\,\,\,\,\,(e > 1)$
Từ những kết quả trên, ta nhận thấy rằng ba đường elip, hypebol, parabol đều có thể được định nghĩa dựa trên tiêu điểm và đường chuẩn. Ba đường đó có tên chung là ba đường conic.
3. Định nghĩa đường cônic
Cho điểm F cố định và đường thẳng $\Delta $ cố định không đi qua F. Tập hợp các điiểm M sao cho tỉ số $\frac{{M{F_0}}}{{d(M;{\Delta _0})}}$ bằng một số dương e cho trước được gọi là đường cônic
Điểm F gọi là tiêu điểm , $\Delta $ gọi là đường chuẩn và e gọi là tâm sai của đường cônic
Từ định nghĩa trên ,kết hợp với tính chất của elip.parabol,hypepol ta có
- Elip là đường cônic tâm sai e < 1
- Parabol là đường cônic có tâm sai e = 1
- Hypebol là đường cônic có tâm sai e >1
|