|
|
1. Định nghĩa phép chiếu song song
Trong không gian cho mp(P) và đường thẳng l cắt mp(P). Với mỗi điểm M
trong không gian vẽ đường thẳng đi qua M và song song hoặc trùng với l
cắt mp(P) tại 1 điểm M’ nào đó
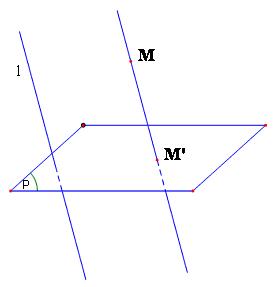
Phép đặt tương ứng mỗi điểm M trong không gian với điểm M’ của mặt phẳng
$\left( P \right)$như trên gọi là phép chiếu song song lên mặt phẳng
$\left( P \right)$ theo phương l.
Mặt phẳng $\left( P \right)$ gọi là mặt phẳng chiếu, đường thẳng l gọi
là phương chiếu; điểm M’ gọi là hình chiếu song song (hoặc ảnh) của điểm
M qua phép chiếu song song nói trên.
Cho hình (H). Tập hợp (H’) gồm hình chiếu song song của tất cả các điểm
thuộc (H) gọi là hình chiếu song song (hoặc ảnh) của hình (H) qua phép
chiếu nói trên.
2. Tính chất
TÍNH CHẤT 1
Hình chiếu song song của một đường thẳng là một đường thẳng
HỆ QUẢ
Hình chiếu song song của một đoạn thẳng là một đoạn thẳng của một tia là một tia.
TÍNH CHẤT 2
Hình chiếu song song của hai đường thẳng song song là hai đường thẳng song song hoặc trùng nhau
TÍNH CHẤT 3
Phép chiếu song song không làm thay đổi tỉ số của hai đoạn thẳng nằm trên hai đường thẳng song song (hoặc trùng nhau).
3. Hình biểu diễn của một hình không gian
ĐỊNH NGHĨA
Hình biểu diễn của một hình (H) trong không gian là hình chiếu song song
của hình (H) trên một mặt phẳng hoặc hình đồng dạng với hình chiếu đó
QUY TẮC (suy ra từ tính chất 3)
Nếu trên hình (H) có hai đoạn thẳng nằm trên hai đường thẳng song song
(hoặc trùng nhau) thì chúng chẳng những được biểu diễn bởi hai đoạn
thẳng nằm trên hai đường thẳng song song (hoặc trùng nhau), mà tỉ số của
hai đoạn thẳng này còn phải bằng tỉ số của hai đoạn thẳng tương ứng
trên hình (H).
CHÚ Ý
Phép chiếu song song nói chung không giữ nguyên tỉ số của hai đoạn thẳng
không nằm trên một đường thẳng) và không giữ nguyên độ lớn của một góc.
Từ đó suy ra nếu trên hình (H) có hai đoạn thẳng không nằm trên hai
đường thẳng song song thì tỉ số của chúng không nhất thiết phải giữ
nguyên trên hình biểu diễn. Cũng như vậy, độ lớn của một góc trên hình H
không nhất thiết được giữ nguyên trên hình biểu diễn
*/ Hình biểu diễn của một đường tròn
Người ta chứng minh được rằng
Hình chiếu song song của một đường tròn là một đường elip hoặc một đường tròn, hoặc đặc biệt có thể là một đoạn thẳng.
Vì vậy, ta thường dùng đường elip làm hình biểu diễn của đường tròn, tâm của elip biểu diễn cho tâm của đường tròn.
|