|
|
1. Vectơ trong không gian
Khái niệm vectơ và các phép toán vectơ đã được đề cập trong chương trình học lớp 10. Tuy nhiên, khi đó tất cả các vectơ mà chúng ta xem xét đều nằm trên cùng một mặt phẳng.
Cho hình hộp $ABCD.A'B'C'D'$ với tâm O
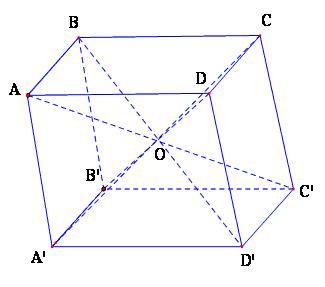
a, Hãy chỉ ra trên hình vẽ những vectơ bằng nhau khác vectơ$\overrightarrow 0 $và kiểm tra tính đúng đắn của đẳng thức
$\overrightarrow {AC'} = \overrightarrow {AB} + \overrightarrow {AD} + \overrightarrow {AA'} $ (1)
b, Chứng minh rằng
$\overrightarrow {AB} + \overrightarrow {B'C'} + \overrightarrow {DD'} = \overrightarrow {AD} + \overrightarrow {D'C'} + \overrightarrow {B'B} = \overrightarrow {A'C} $
CHÚ Ý
Công thức (1) gọi là quy tắc hình hộp (để tìm tổng của ba vectơ)
Ví dụ 1:
Cho tứ diện ABCD
1. Gọi M và N lần lượt là trung điểm của AB và CD. Chứng tỏ rằng
$\overrightarrow {AB} + \overrightarrow {B'C'} + \overrightarrow {DD'} = \overrightarrow {AD} + \overrightarrow {D'C'} + \overrightarrow {B'B} = \overrightarrow {A'C} $ $\overrightarrow {MN} = \frac{1}{2}(\overrightarrow {AD} + \overrightarrow {BC} ) = \frac{1}{2}(\overrightarrow {AC} + \overrightarrow {BD} )$
2. Chứng minh rằng điểm G là trọng tâm của tứ diện ABCD khi và chỉ khi một trong hai điều kiện sau xảy ra:
a, $\overrightarrow {GA} + \overrightarrow {GB} + \overrightarrow {GC} + \overrightarrow {GD} = \overrightarrow 0 $
b, $\overrightarrow {PG} = \frac{1}{4}(\overrightarrow {PA} + \overrightarrow {PB} + \overrightarrow {PC} + \overrightarrow {PD} )$với mọi điểm P
Giải
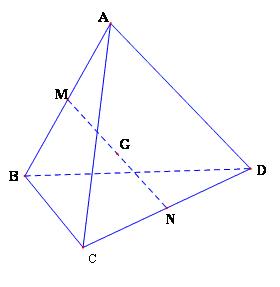
1. Sử dụng quy tắc ba điểm, ta có
$\overrightarrow {MN} = \overrightarrow {MA} + \overrightarrow {AD} + \overrightarrow {DN} $
$\overrightarrow {MN} = \overrightarrow {MB} + \overrightarrow {BC} + \overrightarrow {CN} $
Do $\overrightarrow {MA} + \overrightarrow {MB} = \overrightarrow 0 $
$\overrightarrow {DN} + \overrightarrow {CN} = \overrightarrow 0 $
Nên $\overrightarrow {MN} = \frac{1}{2}(\overrightarrow {AD} + \overrightarrow {BC} )$
Tương tự như trên ta có$\overrightarrow {MN} = \frac{1}{2}(\overrightarrow {AC} + \overrightarrow {BD} )$
2. a, Ta có
$\overrightarrow {GA} + \overrightarrow {GB} = 2\overrightarrow {GM} $
$\overrightarrow {GC} + \overrightarrow {GD} = 2\overrightarrow {GN} $
Điểm G là trọng tâm của tứ diện ABCD khi và chỉ khi
$\overrightarrow {GM} + \overrightarrow {GN} = \overrightarrow 0 \,\,\,hay\,\,\,2(\overrightarrow {GM} + \overrightarrow {GN} ) = \overrightarrow 0 $
Điều này tương đương với $\overrightarrow {GA} + \overrightarrow {GB} + \overrightarrow {GC} + \overrightarrow {GD} = \overrightarrow 0 $
b, G là trọng tâm của tứ diện ABCD khi và chỉ khi
$\overrightarrow {GA} + \overrightarrow {GB} + \overrightarrow {GC} + \overrightarrow {GD} = \overrightarrow 0 $
Điều này có nghĩa là với điểm P bất kỳ, ta có
$\overrightarrow {PA} - \overrightarrow {PG} + \overrightarrow {PB} - \overrightarrow {PG} + \overrightarrow {PC} - \overrightarrow {PG} + \overrightarrow {PD} - \overrightarrow {PG} = \overrightarrow 0 $
Hay $\overrightarrow {PG} = \frac{1}{4}(\overrightarrow {PA} + \overrightarrow {PB} + \overrightarrow {PC} + \overrightarrow {PD} )$
2. Sự đồng phẳng của các vectơ. Điều kiện để 3 vectơ đồng phẳng
ĐỊNH NGHĨA
Ba vectơ gọi là đồng phẳng nếu các giá của chúng cùng song song với một mặt phẳng
Nhận xét
Từ định nghĩa trên, suy ra: Nếu ta vẽ $\overrightarrow {OA} = \overrightarrow a $,$\overrightarrow {OB} = \overrightarrow b $, $\overrightarrow {OC} = \overrightarrow c $ thì ba vectơ $\overrightarrow a ,\,\,\overrightarrow b ,\,\,\overrightarrow c $đồng phẳng khi và chỉ khi bốn điểm O, A, B, C cùng nằm trên một mặt phẳng hay ba đường thẳng OA, OB, OC cùng nằm trong một mặt phẳng
Điều kiện để ba vectơ đồng phẳng
ĐỊNH LÝ 1:
Cho ba vectơ $\overrightarrow a ,\,\,\overrightarrow b ,\,\,\overrightarrow c $, trong đó $\overrightarrow a \,\& \,\overrightarrow b $không cùng phương. Điều kiện cần và đủ để ba vectơ $\overrightarrow a ,\,\,\overrightarrow b ,\,\,\overrightarrow c $đồng phẳng là có các số m, n sao cho $\overrightarrow c = \overrightarrow {ma} + \overrightarrow {nb} $. Hơn nữa, các số m, n là duy nhất
ĐỊNH LÝ 2
Nếu $\overrightarrow a ,\,\,\overrightarrow b ,\,\,\overrightarrow c $là ba vectơ không đồng phẳng thì với mỗi vectơ $\overrightarrow d $, ta tìm được các số m, n, p sao cho $\overrightarrow d = \overrightarrow {ma} + \overrightarrow {nb} + \overrightarrow {pc} $. Hơn nữa, các số m, n, p là duy nhất
|