|
|
1. Phương trình tham số và phương trình chính tắc của đường thẳng
- Trong không gian Oxyz cho đường thẳng d đi qua điểm M0(x0;y0;z0) và có vecto chỉ phương →u(a;b;c)≠0.
Khi đó ta có phương trình tham số của đường thẳng d là:
{x=x0+aty=y0+btz=z0+ct,t∈R (1)
Ngược lại, mỗi phương trình dạng (1) với a2+b2+c2>0 đều là phương trình tham số của đường thẳng d đi qua điểm (x0;y0;z0) và có vecto chỉ phương là →u(a;b;c)
Trong trường hợp abc≠0, khử t từ hệ (1) ta được:
x−x0a=y−y0b=z−z0c; với abc≠0 (2)
Hệ (2) gọi là phương trình chính tắc của đường thẳng d
2. Vị trí tương đối giữa 2 đường thẳng
Trong không gian, cho đường thẳng d đi qua điểm M0, có vecto chỉ phương →u và đường thẳng d’ đi qua điểm M′0 và có vecto chỉ phương →u′ . Vị trí tương đối giữa 2 đường thẳng d và d’:
a) d và d’ trùng nhau khi và chỉ khi 3 vecto →u,→u′,→MoM′0 đôi một cùng phương
⇔[→u,→u′]=[→u,→MoM′0]=→0
b) d và d’ song song khi và chỉ khi →u, →u′ cùng phương nhưng không cùng phương với →MoM′0
⇔{[→u,→MoM′0]≠→0[→u,→u′]=→0
c) d và d’ cắt nhau khi và chỉ khi →u, →u′ không cùng phương, đồng thời 3 vecto →u,→u′,→MoM′0 đồng phẳng
⇔{[→u,→u′]≠0[→u,→u′].→MoM′0=0
d) d và d’ chéo nhau khi và chỉ khi →u,→u′,→MoM′0 không đồng phẳng ⇔[→u,→u′].→MoM′0≠0
3. Một số bài toán về tính khoảng cách
Bài toán 1: Tính khoảng cách h từ 1 điểm M đến đường thẳng d đi qua điểm M0 và có vecto chỉ phương →u
Cách giải:
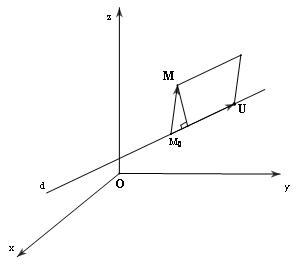
Gọi U là điểm sao cho →M0U=→u
Nếu M không thuộc d thì diện tích S của hình bình hành có 2 cạnh M0M&M0U là : S=|[→M0M,→M0U]|=|[→M0M,→u]|
Vì khoảng cách h cần tìm là chiều cao của hình bình hành ứng với cạnh M0U nên: h=|[→M0M,→u]||→u|
Bài toán 2: Tính khoảng cách h giữa 2 đường thẳng chéo nhau d1&d2 biết d1 đi qua điểm M1 và có vecto chỉ phương →u1; d2 đi qua điểm M2 và có vecto chỉ phương →u2
Cách giải:
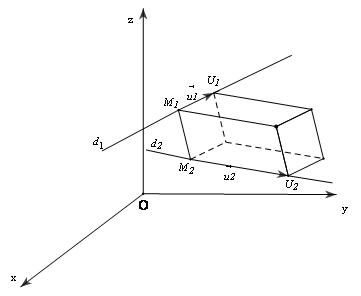
Lấy các điểm U1&U2 sao cho →M1U1=→u1, →M2U2=→u2. Xét hình hộp có 3 cạnh là M1U1,M2U2,M1M2, có thể tích: V=|[→u1,→u2].→M1M2|
Khoảng cách h giữa 2 đường thẳng d1&d2 chính là chiểu cao của hình hộp: h=|[→u1,→u2].→M1M2||[→u1,→u2]|
|