+/ Có: $\overrightarrow{MN}$ (a/6, -2a/3)
=> MN= $\frac{a\sqrt{17}}{6}$ 
+/ Gọi  O(x,y) là tâm $\Delta$MNC
=>  $\overrightarrow{MO}$ (x-a/3, y-2a/3) => $MO^{2}$= $(x-a/3)^{2}+(y-2a/3)^{2}$ (1)
$\overrightarrow{NO}$ (x-a/2, y) => $NO^{2}$= $(x-a/2)^{2}+(y)^{2}$ (2)
$\overrightarrow{CO}$ (x-a, y) => $MO^{2}$= $(x-a)^{2}+(y)^{2}$ (3)
(2), (3)=>  $(x-a/2)^{2}+(y)^{2}$= $(x-a)^{2}+(y)^{2}$
=> x= 3a/4             (4)
(1)(3)=>  $(x-a/3)^{2}+(y-2a/3)^{2}$ = $(x-a)^{2}+(y)^{2}$ (5)
Thay (4) vào (5) được: y= 5a/12
=>  $\overrightarrow{CO}$ (-a/4, 5a/12) => CO= a. $\sqrt{17/72}$

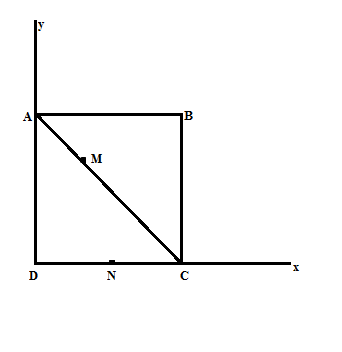Gắn hệ trục tọa độ vào hình vẽ sao cho D trùng với gốc tọa độ O, DC trùng Ox, DA trùng Oy
Khi đó tọa độ các điểm là: D(0,0), A(0,a) , M(a/3, 2a/3), C(a,0), B(a,a), N(a/2,0)
Có: $\overrightarrow{AM}$ (a/3, -a/3), $\overrightarrow{CD}$(-a,0)
=>  $\overrightarrow{AM}$. $\overrightarrow{CD}$= $\frac{-a^{3}}{3}$
Có: $\overrightarrow{BM}$ (-2a/3, -a/3)
=>  $\overrightarrow{BM}$ . $\overrightarrow{CD}$= $\frac{2a^{2}}{3}$

Mỗi bước anh ta tiến một bước hoặc lùi một bước với xác suất như nhau => P(tiến)= P(lùi)= 1/2
Anh ta trở lại điểm xuất phát khi anh ta tiến 4 bước và lùi 4 bước
=> Có xác suất là: P= $C^{4}_{8}.(1/2)^{4}.(1/2)^{4}$ = 35/108

Đường thẳng d đi qua M(2,2,1) có VTCP$\overrightarrow{u}$(1,0,-1)
=> $\begin{cases}x=2+t \\y=2\\ z=1-t \end{cases}$
 A,B $\in $d => A(2+$t_{1}$, 2, 1-$t_{1}$), B (2+$t_{2}$, 2, 1-$t_{2}$)
Vì OAB là tam giác cân tại O=> $OA^{2}=OB^{2}$  
=> $(2+t_{1})^{2}+(1-t_{1})^{2}=(2+t_{2})^{2}+(1-t_{2})^{2}$  => $t_{1}=t_{2}$ hoặc $t_{1}=-t_{2}$ (1)
Có: d(O, AB) = $\frac{\left| {\left[ {\overrightarrow{OA},\overrightarrow{u}} \right]} \right|}{\left| {\overrightarrow{u}} \right|}$  =$\frac{\sqrt{(t_{1}-3)^{2}+13}}{\sqrt{2}}$
Có: $\overrightarrow{AB}$= $(t_{2}-t_{1},-t_{2}+t_{1})$ => AB= $\sqrt{2. (t_{1}-t_{2})^{2}}$
Mà: $S_{OAB}$ = 1/2. d(O,AB). AB = $\frac{\sqrt{17}}{2}$
=> $\sqrt{(t_{1}-3)^{2}+13}.\sqrt{(t_{1}-t_{2})^{2}}=\sqrt{17}$  (2)
Từ (1), (2) => $t_{1}\neq t_{2}$ => $t_{1}=-t_{2}$  (3)
Thay (3) vào (2) ta được:  4.$(t_{1})^{4}$ - 24.$(t_{1})^{3}$+88. $(t_{1})^{2}$- 17=0
Tự tìm $t_{1}$ sẽ biết được $t_{2}$
Từ đó => tọa độ A, B 

Gỉa sử tâm đường tròn là I(x,y, z)
=> $\overrightarrow{OI}$ =(x,y,z) => $OI^{2}$ = $x^{2}+y^{2}+z^{2}$  
$\overrightarrow{AI}$ =(x,y,z-4) => $AI^{2}$ = $x^{2}+y^{2}+(z-4)^{2}$  
$\overrightarrow{BI}$ =(x,y,z) => $BI^{2}$ = $(x-2)^{2}+y^{2}+z^{2}$  
d(I, (P)) = $\frac{\left| {2x+y-z+5} \right|}{\sqrt{6}}$ => $d(I, (P))^{2}$= $\frac{(2x+y-z+5)^{2}}{6}$
Có: $OI^{2}=AI^{2}$=> z=2
$OI^{2}=BI^{2}$=> x=1
$OI^{2}=d(I, (P))^{2}$  => y=1
=> I(1,1,2)
=> $OI^{2}=R^{2}$  =6
=> Phương trình đường tròn: $(x-1)^{2}+(y-1)^{2}+(z-2)^{2}=6$

Để phương trình có 2 nghiệm âm phân biệt thì
$\begin{cases}\Delta>0 \\-b/a <0 \\c/a>0 \end{cases}\\ $
=> $\begin{cases}(2m)^{2}- 4(-4m+4)>0 \\2m <0 \\-4m+4>0 \end{cases}\\ $
 => $\begin{cases}m^{2}+4m-4>0 \\ \\m<1 \end{cases}\\ $
 => $\begin{cases}m< -2-2\sqrt{2} hoặc m> -2+2\sqrt{2} \\ \\m<1 \end{cases}\\ $
 => m<-2-2$\sqrt{2}$ hoặc -2+2$\sqrt{2}$<m<1

Mp(MNP) được mở rộng thành mp(MKE)
Giao điểm của CD với mp(MNP) chính là giao điểm của CD với mp(MKE)
Trong mp(BCD) gọi G =EK $\cap $CD
=> G chính là giao điểm của CD với mp(MNP)

Cắt 2 đường thẳng kia nghĩa là tìm được tọa độ 2 điểm giao nữa. Như vậy ta có được tọa độ 3 điểm, mà qua 3 điểm luôn viết được phương trình đường thẳng trong không gian
Ví dụ: d qua A và hai giao điểm là B,C => vector pháp tuyến của d chính là tích có hướng của $\overrightarrow{AB} và \overrightarrow{AC}$
d qua A và biết được VTPT => phương trình đường thẳng d

Chứng minh đề bài vô lý!
DG cắt BC tại K là trung điểm của BC. Ta cần chứng minh: MI cũng đi qua K
Gỉa sử MI đi qua K => I là trọng tâm $\Delta$BCM, do I là giao điểm của 2 đường trung tuyến MK và BJ => BI= 2/3. BJ
=> I là trọng tâm $\Delta$ABH => AG là đường trung tuyến của $\Delta$ABH (vô lý vì G không là trung điểm của BH )
=> Gỉa sử sai
=> Đề bài sai
=> 3 câu sau không thể làm được bạn nhé :)

Lời giải này có yêu cầu trả vỏ sò để xem. Bạn hãy link trên để vào xem chi tiết

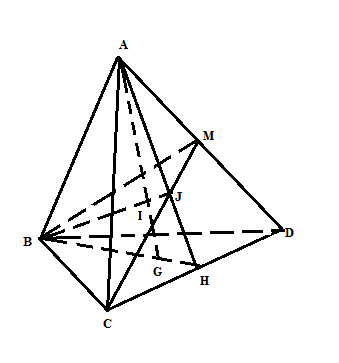a/ Gọi H là trung điểm của CD => G $\in $BH
Trong mp(ACD), gọi J= CM$\cap $AH
=> (BCM)$\cap $(ABH)= BJ
Trong mp(ABH), gọi I= BJ $\cap $AG
=> I là giao của AG và mp(BCM)

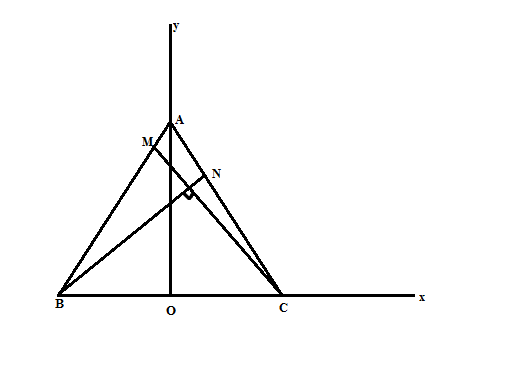Gắn hệ trục tọa độ vào hình vẽ sao cho gốc O trùng với trung điểm của BC, OC trùng với Ox, OA trùng với Oy. Khi đó, tọa độ các điểm sẽ là: C(a/2, 0), B(-a/2,0), A(0, $\frac{a\sqrt{3}}{2}$)
Do, AN= 1/3AC => Tọa độ của N là: N(a/6,$\frac{a\sqrt{3}}{3}$ )
Từ đó, phương trình AB: $\sqrt{3}$x-y+ $\frac{a\sqrt{3}}{2}$=0
M$\in $AB=> M(x, $\sqrt{3}$x+$\frac{a\sqrt{3}}{2}$)
=> $\overrightarrow{CM}$ (x- a/2, $\sqrt{3}$x+$\frac{a\sqrt{3}}{2}$)
Mà $\overrightarrow{BN}$(2a/3, $\frac{a\sqrt{3}}{3}$ )
Vì BN vuông góc với CM => $\overrightarrow{BN}$. $\overrightarrow{CM}$=0 => x= -a/10
=> M(-a/10, $\frac{2a\sqrt{3}}{5}$ )
=> $\overrightarrow{AM}$ (-a/10, $\frac{-a\sqrt{3}}{10}$)
=> AM= a/5

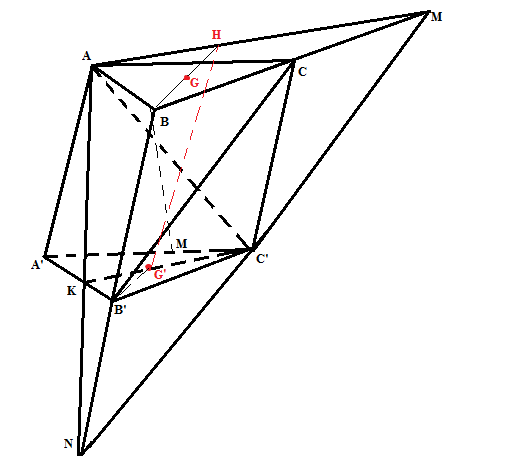c/Ta cần tìm giao điểm của BM và mp(P) nghĩa là ta có thể tìm giao điểm của BM với HG'
Vì M là trung điểm của A'C' => M$\in $B'G
=> BM nằm trong mp(BHMB')
Trong mp(BHMB') gọi J= BM$\cap $HG'
Khi đó, J là giao điểm của BM và mp (P)