a.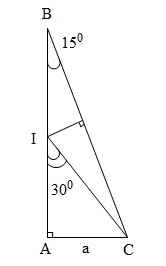

Xét $\Delta ABC$ vuông tại $A$ có $\widehat B = {15^\circ}$
Kẻ trung trực của $BC$ cắt $AB$ tại $I$.
Ta có $\widehat {AIC} = {30^\circ}$. Đặt $AC = a$
Thì $\left\{ \begin{array}{l}
IB = IC = \frac{a}{\sin 30^\circ}=2a\\
AI = a\cot {30^\circ} = a\sqrt 3
\end{array} \right.$
    $ \Rightarrow AB = 2a + a\sqrt 3 $
Suy ra:
•    $c{\rm{o}}{{\rm{s}}^2}{15^\circ} = \frac{1}{{1 + \tan^2 {{15}^\circ}}} = \frac{1}{{8 - 4\sqrt 3 }}$ $ = \frac{{2 + \sqrt 3 }}{4}$
$ \Rightarrow c{\rm{os}}{15^\circ} = \frac{{\sqrt {2 + \sqrt 3 } }}{2} = \frac{{1 + \sqrt 3 }}{{2\sqrt 2 }}$

b) Trong hệ thức Stewart nếu $AM$ là đường trung tuyến thì $BM=CM=\frac{a}{2}$
Suy ra $aMA^2=\frac{a}{2}b^2+\frac{a}{2}c^2-\frac{a^3}{4}\Rightarrow MA^2=\frac{1}{2}b^2+\frac{1}{2}c^2-\frac{a^2}{4}$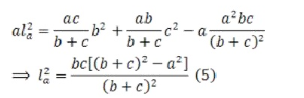



Điều này có nghĩa là
$AD=l_a=\frac{2}{b+c}\sqrt{bcp(p-a)}$

a)

Ta đã biết định lý hàm số  SIN
$\sin A =\frac{a}{2R}$,
định lý hàm số COS
$\cos A= \frac{b^2+c^2-a^2}{2bc}$
và công thức
$abc=4RS$
Vậy
$\tan A = \frac{\sin A}{\cos A}=\frac{2abc}{2R(b^2+c^2-a^2)}=\frac{4S}{b^2+c^2-a^2}$, đpcm.

      $ \cos \left[ {\frac{\pi }{2} - \pi \left( {{x^2} + 2x} \right)} \right] = \sin \left( {\pi {x^2}} \right)$
$ \Leftrightarrow \sin \left[ {\pi \left( {{x^2} + 2x} \right)} \right] = \sin \left( {\pi {x^2}} \right)$
$ \Leftrightarrow  \left[ {\begin{matrix} \pi \left( x^2 + 2x \right) = \pi x^2 + k2 \pi   \\ \pi (x^2 + 2x)  = \pi  - \pi x^2 + k2\pi \end{matrix}} \right.     $$ \Leftrightarrow \left[ {\begin{matrix} x = k \in \mathbb{Z}  \\ 2x^2 + 2x - \left( 2k + 1 \right) = 0  \end{matrix}} \right.  $$\left( {\text{*}} \right)$
Do $\begin{cases}\left( {\text{*}} \right)  \\x{\text{ > }}0  \\k \in \mathbb{Z}  \\\end{cases}  $   suy ra $x=\frac{-b +\sqrt{\Delta}}{2a}=\frac{-1 +\sqrt{4k+3}}{2}$
Để $x$ dương và nhỏ nhất với $k \in \mathbb{Z}$ và $4k+3 \ge 0$ thì cần $k=0.$
Vậy $\min x = \frac{{\sqrt 3  - 1}}{2}$

a)
Ta có
$\begin{cases}CD \parallel AB, CD=AB\\ EF \parallel AB, EF=AB \end{cases}\Rightarrow CD \parallel EF, CD=EF$
suy ra $DCEF$ là hình bình hành nên $DF \parallel CE$.
Ta có
$ OD \parallel O'F, OD=O'F$
suy ra $DOO'F$ là hình bình hành nên $DF \parallel OO'$.
Và ta có đpcm.

b) Vì $O$ là giao điểm của hai đường chéo nên $O$ là trung điểm mỗi đường.
Từ câu a suy ra $P, Q$ lần lượt là trung điểm của $CD, AB$.
Theo tính chất đường trung bình thì hiển nhiên có đpcm.

a) Ta dễ thấy
$\begin{cases}MO \parallel SB \rightarrow MO \parallel mp(SBC) \\NO \parallel SC \rightarrow NO \parallel mp(SBC) \end{cases} \Rightarrow mp(OMN) \parallel mp(SBC)$
do hai mặt phẳng $MNO$ và $ABCD$ có chung điểm $O$ nên suy ra chúng cắt nhau theo giao tuyến $(d) \parallel BC.$

Trước hết ta cần điều kiện $\begin{cases}x>0 \\ x+2>0 \end{cases}\Leftrightarrow x>0$
Để biểu thức có nghĩa thì cần có
$\lg x + \lg (x+2) \ge 0\Leftrightarrow \lg x(x+2) \ge 0\Leftrightarrow x(x+2) \ge 1$, do hàm $\lg$ là hàm logarit cơ số $10>1$ nên là hàm đồng biến.
Ta có
$\begin{cases}x>0 \\  x^2+2x-1 \ge 0 \end{cases}\Leftrightarrow \boxed{x \ge \sqrt 2 -1}$

Khai triển và rút gọn thì BĐT cần chứng minh tương đương với
\[
\sum_{sym}a^6 + 2\sum_{sym}a^5b + 2\sum_{sym}a^3b^3 + \sum_{sym}a^4bc + 4\sum_{sym}a^3b^2c \geq 6\sum_{sym}a^4b^2 + 4\sum_{sym}a^2b^2c^2
\]
Sử dụng BĐT Schur và Muirhead ta có
$$\sum_{sym}a^6 + \sum_{sym}a^4bc \geq 2\sum_{sym}a^5b \geq 2\sum_{sym}a^4b^2$$
Sử dụng BĐT Muirhead tiếp tục ta được 
$$2\sum_{sym}a^5b + 2\sum_{sym}a^3b^3 + 4\sum_{sym}a^3b^2c \geq 4\sum_{sym}a^4b^2 + 4\sum_{sym}a^2b^2c^2$$
Và ta có đpcm.

Xét hai trường hợp :
*Trường hợp $1:$ Nếu $k=1$ thì :
$\overrightarrow {M'N'}=\overrightarrow {MN}\Rightarrow  MNN'M'  $ là hình bình hành $\Rightarrow  \overrightarrow {MM'}=\overrightarrow {NN'}  $
suy ra $M',N'$ theo thứ tự là ảnh của $M,N$ trong phép tịnh tiến theo véctơ $\overrightarrow {v}=\overrightarrow {MM'}  $
Vậy trong trường hợp này $F$ là một phép tịnh tiến

*Trường hợp $2:$ Nếu $k\neq  1$ thì đẳng thức $\overrightarrow {M'N'}=k\overrightarrow {MN}  $ suy ra :
$MN//M'N'$ và $MN\neq  M'N'$ nên $MM'\cap NN'=\left\{ {O} \right\} $
Từ đó ta nhận được :
$\frac{OM'}{OM}=\frac{ON'}{ON}=\frac{MM'}{NN'}=k   $
$\Rightarrow  \overrightarrow {OM'}=k\overrightarrow {OM}  $ và $\overrightarrow {ON'}=k\overrightarrow {ON}  $
suy ra $M',N'$ theo thứ tự là ảnh của $M,N$ trong phép vị tự tâm $O$ tỉ số $k$

Đặt $t= \frac{\pi}{2}-x \Rightarrow dt=-dx, x=0 \rightarrow t= \frac{\pi}{2}, x= \frac{\pi}{2}\rightarrow t=0$
$I= \int_{0}^{\pi /2}\frac{\sin ^{2012}x}{\sin ^{2012}x + \cos ^{2012}x}dx$
$I= -\int_{\pi /2}^{0}\frac{\sin ^{2012}\left (  \frac{\pi}{2}-t \right )}{\sin ^{2012}\left (  \frac{\pi}{2}-t \right ) + \cos ^{2012}\left (  \frac{\pi}{2}-t \right )}dt$
$I= \int_{0}^{\pi /2}\frac{\cos ^{2012}t}{\cos ^{2012}t+ \sin ^{2012}t}dt$
$I= \int_{0}^{\pi /2}\left[ {1-\frac{\sin ^{2012}t}{\cos ^{2012}t+ \sin ^{2012}t}} \right]dt$
$I= \int_{0}^{\pi /2}dt-I$
$\boxed{I=\frac{\pi}{4}}$

b. Nếu đúng đề như thế này thì ta cần điều kiện
$\begin{cases}x^3+8 \ge 0\\ x^2+3x+2 \ge 0 \end{cases}\Leftrightarrow x \ge -1$
Với điều kiện này thì bình phương hai vế ta được
      $4(x+1)^2(x+2)^2=9(x+2)(x^2-4x+4)$
$\Leftrightarrow 4(x+1)^2(x+2)=9(x^2-4x+4)$
$\Leftrightarrow 4x^3+7x^2+38x-28=0$
Đây là PT bậc ba có nghiệm không đẹp. Bạn có thể xem cách giải tổng quát trong Toán nân cao và Phát Triển 9 tập 2 của tác giả Vũ Hữu bình nhé.
Đây là kết quả

c. Điều kiện $x \ge -1$
Đặt $a=\sqrt{x+1}, b=\sqrt{x^2-x+1}\Rightarrow \begin{cases}ab=\sqrt{x^3+1} \\ a^2+b^2=x^2+2 \end{cases}$
Như vậy PT đã cho
$2a^2+2b^2=5ab\Leftrightarrow 2a^2-ab-4ab+2b^2=0\Leftrightarrow (a-2b)(2a-b)=0$
+ Nếu $a=2b\Leftrightarrow \sqrt{x+1}=2\sqrt{x^2-x+1}\Leftrightarrow x+1=4x^2-4x+4\Leftrightarrow 4x^2-5x+3=0$, vô nghiệm.
+ Nếu $2a=b\Leftrightarrow 2\sqrt{x+1}=\sqrt{x^2-x+1}\Leftrightarrow 4x+4=x^2-x+1\Leftrightarrow x^2-5x-3=0\Leftrightarrow x=\frac{1}{2}\left ( 5 \pm \sqrt {37} \right )$

Ta có
$ (1-a^2)(1-b) \ge 0\Leftrightarrow \ a^2 b \ge a^2 +b -1$
$ \Rightarrow a^2 b +b^2 c+c^2a \ge \sum{a^2} + \sum a -3 \ge \sum{a^3} + \sum a^3 -3=2\sum{a^3}  -3$
Như vậy
Vế trái $=2 \sum{a^3} -(a^2 b +b^2 c+c^2a)  \le 3$, đpcm.
Đẳng thức xảy ra khi $(a,b,c) \in \left\{ {(1,1,1); (1,1,0)} \right\}$ và các hoán vị của nó.