|
|
giải đáp
|
hình 11
|
|
|
|
3/ Gọi I là trung điểm của SC. Ta sẽd chứng minh I cách đều 5 điểm S, A,B, C, D
$\Delta$ SBC, $\Delta$ SAC, $\Delta$ SDC là các tam giác vuông => IS= IC=IB=IA=ID= 1/2 SC
Như vậy, I cách đều 5 điểm S, A,B, C,D.
|
|
|
|
giải đáp
|
hình 11
|
|
|
|
2/ BC vuông góc với mp(SAB) => BC vuông góc với AH, MÀ AH vuông góc với SB => AH vuông góc với mp(SBC)=> AH vuông góc với SC(1)
DC vuông góc với mp(SAD) => DC vuông góc với AE, MÀ AE vuông góc với SD => AE vuông góc với mp(SDC)=> AE vuông góc với SC (2)
Theo giả thiết AK vuông góc với SC (3)
(1)(2)(3)=> AE, AK, AH cùng nằm trên mp vuông góc với SC
=> A, E, K, H đồng phẳng (đpcm)
|
|
|
|
giải đáp
|
hình 11
|
|
|
|
1/ SA vuông góc với đáy
=> SA vuông góc với AB => $\Delta$SAB là tam giác vuông
SA vuông góc với AD => $\Delta$SAD là tam giác vuông
SA vuông góc với BC mà BC vuông góc với AB => BC vuông góc với mp(SAB) => BC vuông góc với SB => $\Delta$ SBC là tam giác vuông
SA vuông góc với DC mà DC vuông góc với AD => DC vuông góc với mp(SAD) => DC vuông góc với SD => $\Delta$ SDC là tam giác vuông
|
|
|
|
sửa đổi
|
hình 11
|
|
|
|
hình 11 Cho hình chóp S.ABCD, đáy (ABCD) là hình chữ nhật. H, K, E lần lượt là hình chiếu vuôn góc của A lên SB, SC, SD.1, C/m: các mặt bên của hình chóp là các tam giác vuông2, C/m: AH vuông góc (SBC). Từ đó suy ra 4 điểm A, H, K, E đồng phẳng3, Tìm điểm cách đều 5 điểm S, A, B, C, D4, Tìm điểm cách đều 7 điểm A, B, C, D, H, K, E
hình 11 Cho hình chóp S.ABCD, đáy (ABCD) là hình chữ nhật , SA vuông góc với mp (ABCD). H, K, E lần lượt là hình chiếu vuôn góc của A lên SB, SC, SD.1, C/m: các mặt bên của hình chóp là các tam giác vuông2, C/m: AH vuông góc (SBC). Từ đó suy ra 4 điểm A, H, K, E đồng phẳng3, Tìm điểm cách đều 5 điểm S, A, B, C, D4, Tìm điểm cách đều 7 điểm A, B, C, D, H, K, E
|
|
|
|
bình luận
|
câu hỏi toán học
Đề bài bạn đưa ra đã có những lời giải rất tốt vì trình bày được theo nhiều cách khác nhau, đây là giải theo phương pháp tọa độ lớp 12, lời giải của bạn Khang là theo cách tính trực tiếp lớp 11.
|
|
|
|
|
|
|
|
sửa đổi
|
câu hỏi toán học
|
|
|
|
Xét $\Delta$A'AC vuông tại A => $AC^{2}= (3a)^{2}- (2a)^{2}= 5a^{2}$Xét $\Delta$ABC vuông tại B => $BC^{2}= 5a^{2}- a^{2}= 4a^{2}$ => BC= 2aGắn hệ trục tọa độ vào hình vẽ sao cho B trùng gốc tọa độ, BA trùng Ox, BC trùng Oy, BB' trùng OzKhi đó tọa độ các điểm là: B(0,0,0), A'(a, 0, 2a), C(0, 2a, 0), A(a, 0,0), M(a/2, a, 2a)=> $\overrightarrow{AM}$ (-a/2, a, 2a)= (-1,2,4) => Phương trình AM $\begin{cases}x= a-t_{1} \\ y=2t_{1}\\z=4t_{1} \end{cases}$$\overrightarrow{A'C}$ (-a, 2a, -2a)= (1,-2,2) => Phương trình A'C $\begin{cases}x= t_{2} \\ y= 2a-2t_{2}\\z=2t_{2} \end{cases}$Có: I= AM$\cap $A'C => Tọa độ I thỏa mãn : $\begin{cases}a-t_{1}= t_{2} \\ 2t_{1}=2a-2t_{2}\\4t_{1}=2t_{2} \end{cases}$ => $\begin{cases} t_{1}= a/3\\ t_{2}= 2a/3 \end{cases}$=> I(2a/3, 2a/3, 4a/3)Lại có phương trình mp(A'AB) là: y=0=> d(I, (A'AB)) = $\frac{\left| {2a/3} \right|}{\sqrt{1}}$= 2a/3Mà: $S_{A'AB}$ = 1/2. AA'. AB= $a^{2}$=> $V_{IAA'B}$= 1/3. d(I, (A'AB)) . $S_{A'AB}$ = $\frac{2a^{2}}{9}$
Xét $\Delta$A'AC vuông tại A => $AC^{2}= (3a)^{2}- (2a)^{2}= 5a^{2}$Xét $\Delta$ABC vuông tại B => $BC^{2}= 5a^{2}- a^{2}= 4a^{2}$ => BC= 2aGắn hệ trục tọa độ vào hình vẽ sao cho B trùng gốc tọa độ, BA trùng Ox, BC trùng Oy, BB' trùng OzKhi đó tọa độ các điểm là: B(0,0,0), A'(a, 0, 2a), C(0, 2a, 0), A(a, 0,0), M(a/2, a, 2a)=> $\overrightarrow{AM}$ (-a/2, a, 2a)= (-1,2,4) => Phương trình AM $\begin{cases}x= a-t_{1} \\ y=2t_{1}\\z=4t_{1} \end{cases}$$\overrightarrow{A'C}$ (-a, 2a, -2a)= (1,-2,2) => Phương trình A'C $\begin{cases}x= t_{2} \\ y= 2a-2t_{2}\\z=2t_{2} \end{cases}$Có: I= AM$\cap $A'C => Tọa độ I thỏa mãn : $\begin{cases}a-t_{1}= t_{2} \\ 2t_{1}=2a-2t_{2}\\4t_{1}=2t_{2} \end{cases}$ => $\begin{cases} t_{1}= a/3\\ t_{2}= 2a/3 \end{cases}$=> I(2a/3, 2a/3, 4a/3)Lại có phương trình mp(A'AB) là: y=0=> d(I, (A'AB)) = $\frac{\left| {2a/3} \right|}{\sqrt{1}}$= 2a/3Mà: $S_{A'AB}$ = 1/2. AA'. AB= $a^{2}$=> $V_{IAA'B}$= 1/3. d(I, (A'AB)) . $S_{A'AB}$ = $\frac{2a^{2}}{9}$
|
|
|
|
giải đáp
|
câu hỏi toán học
|
|
|
|
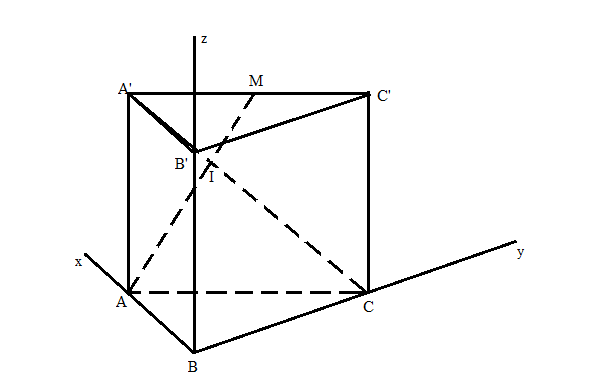 Xét $\Delta$A'AC vuông tại A => $AC^{2}= (3a)^{2}- (2a)^{2}= 5a^{2}$ Xét $\Delta$ABC vuông tại B => $BC^{2}= 5a^{2}- a^{2}= 4a^{2}$ => BC= 2a Gắn hệ trục tọa độ vào hình vẽ sao cho B trùng gốc tọa độ, BA trùng Ox, BC trùng Oy, BB' trùng Oz Khi đó tọa độ các điểm là: B(0,0,0), A'(a, 0, 2a), C(0, 2a, 0), A(a, 0,0), M(a/2, a, 2a) => $\overrightarrow{AM}$ (-a/2, a, 2a)= (-1,2,4) => Phương trình AM $\begin{cases}x= a-t_{1} \\ y=2t_{1}\\z=4t_{1} \end{cases}$ $\overrightarrow{A'C}$ (-a, 2a, -2a)= (1,-2,2) => Phương trình A'C $\begin{cases}x= t_{2} \\ y= 2a-2t_{2}\\z=2t_{2} \end{cases}$ Có: I= AM$\cap $A'C => Tọa độ I thỏa mãn : $\begin{cases}a-t_{1}= t_{2} \\ 2t_{1}=2a-2t_{2}\\4t_{1}=2t_{2} \end{cases}$ => $\begin{cases} t_{1}= a/3\\ t_{2}= 2a/3 \end{cases}$ => I(2a/3, 2a/3, 4a/3) Lại có phương trình mp(A'AB) là: y=0 => d(I, (A'AB)) = $\frac{\left| {2a/3} \right|}{\sqrt{1}}$= 2a/3 Mà: $S_{A'AB}$ = 1/2. AA'. AB= $a^{2}$ => $V_{IAA'B}$= 1/3. d(I, (A'AB)) . $S_{A'AB}$ = $\frac{2a^{2}}{9}$ |
|
|
|
sửa đổi
|
Bài toán mặt phẳng song song với mặt phẳng(1).
|
|
|
|
1a) Gọi $M,N$ lần lượt là trung điểm của $BC',CC'$ thì $\dfrac{AG_1}{AN}=\dfrac{AG_2}{AM}=\dfrac{2}{3}\Rightarrow G_1G_2 \parallel MN \Rightarrow G_1G_2 \parallel (BCC'B')$
1a) Gọi $M,N$ lần lượt là trung điểm của $BC,CC'$ thì $\dfrac{AG_1}{AN}=\dfrac{AG_2}{AM}=\dfrac{2}{3}\Rightarrow G_1G_2 \parallel MN \Rightarrow G_1G_2 \parallel (BCC'B')$
|
|
|
|
giải đáp
|
cấp số cộng
|
|
|
|
Trong cấp số cộng thì 1 số bằng trung bình cộng 2 số liền kề
=> a= $\frac{-1+3}{2}$= 1
Khi đó: 3= $\frac{1+b}{2}$ => b=5
|
|
|
|
|
|
sửa đổi
|
hơi khó các anh ạ
|
|
|
|
b/ Ý tưởng chứng minh: Để chứng minh 2 mp vuông góc với nhau ta chứng minh trong 2 mp đó chứa 2 cặp cạnh vuông góc với nhau.+) Chứng minh: (SAB) vuông góc với (SAD)AB vuông góc với AD, AB vuông góc với SA => AB vuông góc với (SAD)=> AB vuông góc với SD (1)AD vuông góc với AB, AD vuông góc với SA => AD vuông góc với (SAB)=> AD vuông góc với SB (2)(1)(2) => (SAB) vuông góc với (SAD)+) Chứng minh: (SAC) vuông góc với (SCD) tương tự như trêngợi ý :
b/ Ý tưởng chứng minh: Để chứng minh 2 mp vuông góc với nhau ta chứng minh trong 2 mp đó chứa 2 cặp cạnh vuông góc với nhau.+) Chứng minh: (SAB) vuông góc với (SAD)AB vuông góc với AD, AB vuông góc với SA => AB vuông góc với (SAD)=> AB vuông góc với SD (1)AD vuông góc với AB, AD vuông góc với SA => AD vuông góc với (SAB)=> AD vuông góc với SB (2)(1)(2) => (SAB) vuông góc với (SAD)+) Chứng minh: (SAC) vuông góc với (SCD) tương tự như trêngợi ý :
|
|
|
|
giải đáp
|
hơi khó các anh ạ
|
|
|
|
b/ Ý tưởng chứng minh: Để chứng minh 2 mp vuông góc với nhau ta chứng minh trong 2 mp đó chứa 2 cặp cạnh vuông góc với nhau. +) Chứng minh: (SAB) vuông góc với (SAD) AB vuông góc với AD, AB vuông góc với SA => AB vuông góc với (SAD)=> AB vuông góc với SD (1) AD vuông góc với AB, AD vuông góc với SA => AD vuông góc với (SAB)=> AD vuông góc với SB (2) (1)(2) => (SAB) vuông góc với (SAD) +) Chứng minh: (SAC) vuông góc với (SCD) tương tự như trên gợi ý : 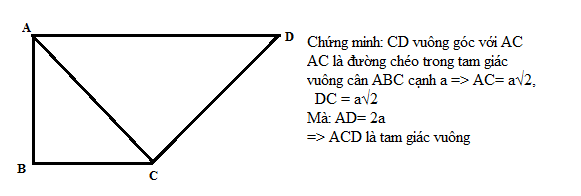 |
|
|
|
giải đáp
|
hơi khó các anh ạ
|
|
|
|
a/ (SAB) vuông góc với mp (ABCD)
(SAD) vuông góc với mp(ABCD)
=> đường vuông góc chung của 2 mp(SAB) và mp(SAD) là SA vuông góc với (ABCD) (đpcm)
|
|
|
|
giải đáp
|
Bài toán mặt phẳng song song với mặt phẳng(2).
|
|
|
|
c/ Trong mp(ABB'A'), kẻ MG//PN (G$\in $BB')
Khi đó: MPNG chính là thiết diện của (MNP) với hình hộp
Ta có: MPNG là hình bình hành (vì dễ dàng chứng minh được MG=PN)
P/S: lời giải này được áp dụng cho chương trình lớp 12!
|
|
|
|