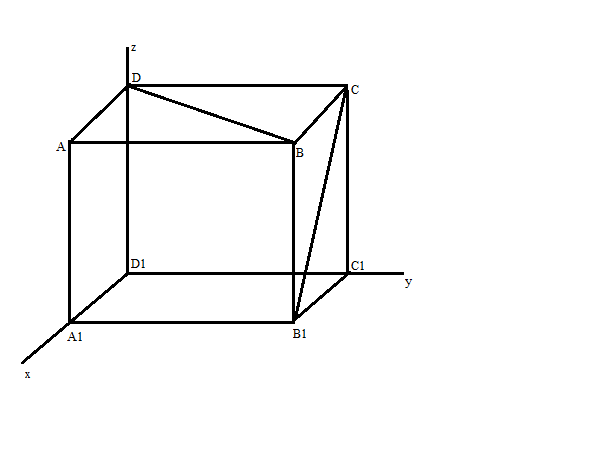Gắn hệ trục tọa độ vào hình vẽ sao cho $D_{1}$ trùng với gốc tọa độ O, $D_{1}A_{1}$ trùng với Ox, $D_{1}C_{1}$ trùng với Oy, $D_{1}D_{}$ trùng với Oz
Khi đó tọa độ các điểm là: D(0,0,a), B(a,a,a), C(0,a,a), $B_{1}$(a,a,0)
=> Khoảng cách giữa BD và $CB_{1}$ là: h= $\frac{\left| {\left[ {\overrightarrow{BD},\overrightarrow{CB_{1}}} \right].\overrightarrow{CD}} \right|}{\left| {\left[ {\overrightarrow{BD},\overrightarrow{CB_{1}}} \right]} \right|}$ = $\frac{a}{\sqrt{3}}$

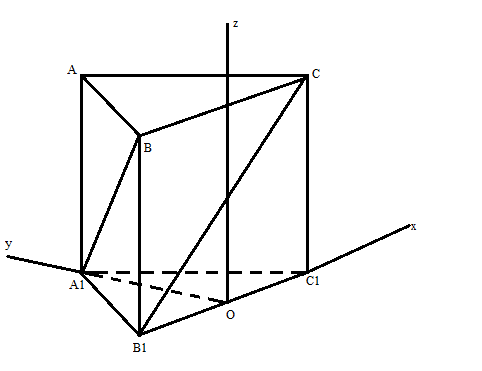Gắn hệ trục tọa độ vào trong hình vẽ sao cho trung điểm O của $B_{1}C_{1}$ chính là gốc tọa độ, $OC_{1}$ trùng với Ox, $OA_{1}$ trùng với Oy, Oz vuông góc với mp ($A_{1}B_{1}C_{1}$) và cùng chiều với hình chóp
Khi đó tọa độ các điểm là: C(a/2, 0,a), B1(-a/2,0,0), B(-a/2,0 ,a), A1(0,$\frac{a\sqrt{3}}{2}$,0)
Khi đó, khoảng cách giưã $CB_{1}$ và $BA_{1}$ là: h= $\frac{\left| {\left[ {\overrightarrow{BA_{1}},\overrightarrow{CB_{1}}} \right]. \overrightarrow{BC}} \right|}{\left| {\left[ {\overrightarrow{CB_{1}},\overrightarrow{BA_{1}}} \right]} \right|}$ = $\frac{3a}{\sqrt{66}}$

Chọn ngẫu nhiên 3 viên mà có cả bi đỏ và bi xanh có số cách là: 
+/ 1 đỏ, 1 xanh, 1 vàng: $C^{1}_{6}.C^{1}_{5}.C^{1}_{4}$ = 120
+/ 1 đỏ, 2 xanh:  $C^{1}_{6}.C^{2}_{5}$= 60
+/ 2 đỏ, 1 xanh:  $C^{2}_{6}.C^{1}_{5}$= 75
=> Có tổng số cách chọn thỏa mãn là: 120+60+75 =255 

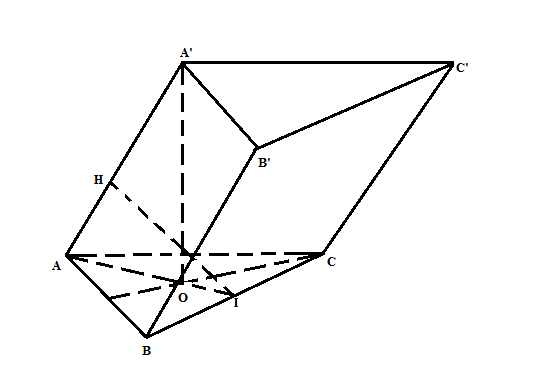Gọi I là trung điểm của BC
Trong mp(A'AI) kẻ IH vuông góc với AA' (H$\in $AA')
Ta có: BC vuông góc với AI, BC vuông góc với A'O => BC vuông góc với (A'AI) => BC vuông góc với IH
=> IH là đường vuông góc chung của BC và AA' => IH= $\frac{a\sqrt{3}}{8}$ 
Có AI là trung tuyến trong $\Delta$ABC đều cạnh a => AI= $\frac{a\sqrt{3}}{2}$ 
Xét $\Delta$AHI vuông tại H => sin HAI= HI/ AI => 1/4
Xét $\Delta A'OA$ vuông tại O  => A'O= OA. tan HAI= $\frac{a\sqrt{3}}{3}$. $\frac{1}{\sqrt{15}}$ = $\frac{a}{3\sqrt{5}}$
=> $V_{lăng trụ}$ =  A'O. $S_{ABC}$= $\frac{a}{3\sqrt{5}}$. $\frac{a^{2}.\sqrt{3}}{4}$= $\frac{a^{3}.\sqrt{15}}{60}$

+/ Có: $\overrightarrow{MN}$ (a/6, -2a/3)
=> MN= $\frac{a\sqrt{17}}{6}$ 
+/ Gọi  O(x,y) là tâm $\Delta$MNC
=>  $\overrightarrow{MO}$ (x-a/3, y-2a/3) => $MO^{2}$= $(x-a/3)^{2}+(y-2a/3)^{2}$ (1)
$\overrightarrow{NO}$ (x-a/2, y) => $NO^{2}$= $(x-a/2)^{2}+(y)^{2}$ (2)
$\overrightarrow{CO}$ (x-a, y) => $MO^{2}$= $(x-a)^{2}+(y)^{2}$ (3)
(2), (3)=>  $(x-a/2)^{2}+(y)^{2}$= $(x-a)^{2}+(y)^{2}$
=> x= 3a/4             (4)
(1)(3)=>  $(x-a/3)^{2}+(y-2a/3)^{2}$ = $(x-a)^{2}+(y)^{2}$ (5)
Thay (4) vào (5) được: y= 5a/12
=>  $\overrightarrow{CO}$ (-a/4, 5a/12) => CO= a. $\sqrt{17/72}$