|
|
|
|
sửa đổi
|
đã đăng bài này mà không thấy ai giải hộ, các ad đi đâu rùi.hjx
|
|
|
|
Có 10 cặp vợ chồng( mỗi cặp là 1 phụ nữ, 1 đàn ông), phụ nữ không bắt tay với phụ nữ, vợ chồng không bắt tay nhau=> mỗi người phụ nữ sẽ bắt tay với 9 người đàn ông còn lại (không phải chồng mình), có 9 người phụ nữ như vậy.Do đó có: 9.9=81 cái bắt tay.
Có 10 cặp vợ chồng( mỗi cặp là 1 phụ nữ, 1 đàn ông), phụ nữ không bắt tay với phụ nữ, vợ chồng không bắt tay nhauTH1: mỗi người phụ nữ sẽ bắt tay với 9 người đàn ông còn lại (không phải chồng mình), có 9 người phụ nữ như vậy.Do đó có: 9.9=81 cái bắt tay. TH2: 10 người đàn ông bắt tay nhau => có 9+8+7+6+5+4+3+2+1=45 cái bắt tayVậy tổng số cái bắt tay là :45+81=126 cái bắt tay
|
|
|
|
|
|
giải đáp
|
đã đăng bài này mà không thấy ai giải hộ, các ad đi đâu rùi.hjx
|
|
|
|
Có 10 cặp vợ chồng( mỗi cặp là 1 phụ nữ, 1 đàn ông), phụ nữ không bắt tay với phụ nữ, vợ chồng không bắt tay nhau
TH1: mỗi người phụ nữ sẽ bắt tay với 9 người đàn ông còn lại (không phải chồng mình), có 9 người phụ nữ như vậy.
Do đó có: 9.9=81 cái bắt tay.
TH2: 10 người đàn ông bắt tay nhau => có 9+8+7+6+5+4+3+2+1=45 cái bắt tay
Vậy tổng số cái bắt tay là :45+81=126 cái bắt tay
|
|
|
|
sửa đổi
|
Hình học không gian về hinh lăng trụ
|
|
|
|
a/ AA' vuông hóc với mp (ABC)=> ABC.A'B'C' là lăng trụ đứngGọi G là hình chiếu vuông góc của N xuống mp (ABC) => G là trung điểm của BCXét $\Delta$NGM vuông tại G, $\widehat{NMG}$ =$\alpha$=> NG= MN. sin$\widehat{NMG}$= a. sin$\alpha$ MG= a.cos$\alpha$ => Hình lăng trụ có các cạnh bên: AA'= BB'= CC'= NG= a. sin$\alpha$Các cạnh mặt đáy hình lăng trụ: AC=AB= 2.MG= 2.a.cosαBC= AC.$\sqrt{2}$= 2.$\sqrt{2}$.a.cosα
a/ AA' vuông hóc với mp (ABC)=> ABC.A'B'C' là lăng trụ đứngGọi G là hình chiếu vuông góc của N xuống mp (ABC) => G là trung điểm của BCXét $\Delta$NGM vuông tại G, $\widehat{NMG}$ =$\alpha$=> NG= MN. sin$\widehat{NMG}$= a. sin$\alpha$ MG= a.cos$\alpha$ => Hình lăng trụ có các cạnh bên: AA'= BB'= CC'= NG= a. sin$\alpha$Các cạnh mặt đáy hình lăng trụ: AC=AB= 2.MG= 2.a.cosαBC= AC.$\sqrt{2}$= 2.$\sqrt{2}$.a.cosα
|
|
|
|
giải đáp
|
Hình học không gian về hinh lăng trụ
|
|
|
|
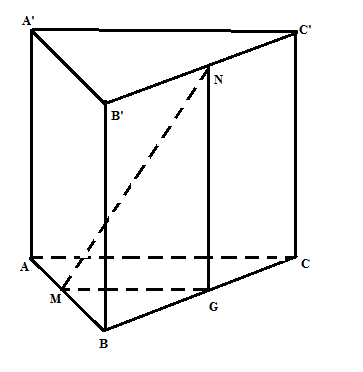 a/ AA' vuông hóc với mp (ABC)=> ABC.A'B'C' là lăng trụ đứng Gọi G là hình chiếu vuông góc của N xuống mp (ABC) => G là trung điểm của BC Xét $\Delta$NGM vuông tại G, $\widehat{NMG}$ =$\alpha$ => NG= MN. sin$\widehat{NMG}$= a. sin$\alpha$ MG= a.cos$\alpha$ => Hình lăng trụ có các cạnh bên: AA'= BB'= CC'= NG= a. sin$\alpha$ Các cạnh mặt đáy hình lăng trụ: AC=AB= 2.MG= 2.a.cos α
BC= AC.$\sqrt{2}$= 2.$\sqrt{2}$.a.cos α
|
|
|
|
sửa đổi
|
Hình học không gian về hinh lăng trụ
|
|
|
|
Hình học không gian về hinh lăng trụ cho hình lăng trụ ABC.A'B"C' đáy ABC là tam giác vuông cân đỉnh A ,AA' vuông góc với mp (ABC) . M,N là trung điểm AB,B'C', MN =a .MN hợp với mp(ABC) góc $\alpha$ và hợp với mp (BCC C'B') góc $\beta$a, tính cạnh đáy là cạnh bên hình lăng trụb. CMR : cos$\alpha$ = $\sqrt{2}$ sin$\beta$
Hình học không gian về hinh lăng trụ cho hình lăng trụ ABC.A'B"C' đáy ABC là tam giác vuông cân đỉnh A ,AA' vuông góc với mp (ABC) . M,N là trung điểm AB,B'C', MN =a .MN hợp với mp(ABC) góc $\alpha$ và hợp với mp (BCC'B') góc $\beta$a, tính cạnh đáy và cạnh bên hình lăng trụb. CMR : cos$\alpha$ = $\sqrt{2}$ sin$\beta$
|
|
|
|
sửa đổi
|
Bài toán về đường thẳng song song với mặt phẳng.
|
|
|
|
a/ Có MN là đường trung bình trong hình bình hành ABCD => MN// BC, MN// AD => MN// (SBC), MN//(SCD) (đpcm)b/ Có IM là đường trung bình trong $\Delta$SAB => IM// SBMặt khác, MN// BCMà: IM, MN nằm trong (IMN); SB, BC nằm trong(SBC)=> (SBC)//(IMN)=> SB, SC // (IMN) (đpcm)
a/ Có MN là đường trung bình trong hình bình hành ABCD => MN// BC, MN// AD => MN// (SBC), MN//(SCD) (đpcm)b/ Có IM là đường trung bình trong $\Delta$SAB => IM// SBMặt khác, MN// BCMà: IM, MN nằm trong (IMN); SB, BC nằm trong(SBC)=> (SBC)//(IMN)=> SB, SC // (IMN) (đpcm)
|
|
|
|
giải đáp
|
Bài toán về đường thẳng song song với mặt phẳng.
|
|
|
|
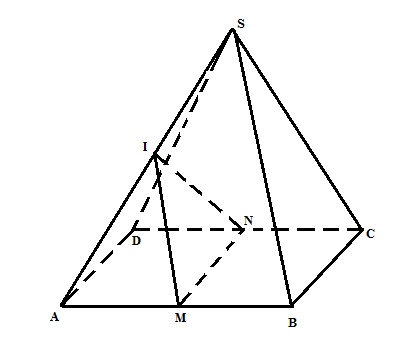 a/ Có MN là đường trung bình trong hình bình hành ABCD => MN// BC, MN// AD => MN// (SBC), MN//(SCD) (đpcm) b/ Có IM là đường trung bình trong $\Delta$SAB => IM// SB Mặt khác, MN// BC Mà: IM, MN nằm trong (IMN); SB, BC nằm trong(SBC) => (SBC)//(IMN) => SB, SC // (IMN) (đpcm) |
|
|
|
giải đáp
|
Giải Giúp e e cần gấp !!!!
|
|
|
|
Áp dụng hệ thức lượng trong tam giác: $a^{2}$= $b^{2}$+$c^{2}$- 2.bc.cosA= $3^2$ => a=4$\sqrt{2}$
Do cosA= $3/5$=> sinA= $4/5$
=> S=$\frac{1}{2}$.b.c. sinA= 14= $\frac{1}{2}$.HA.a => HA= $\frac{7}{\sqrt{2}}$ (HA là đường cao hạ từ đỉnh A)
Bán kính đường tròn ngoại tiếp tam giác R thỏa mãn hệ thức lượng:
a= 2R.sinA => R=$\frac{5\sqrt{2}}{2}$
|
|
|
|
sửa đổi
|
có bạn nào giúp mình k
|
|
|
|
$V_{SABC}$= 1/3. SA.$S_{ABC}$= 1/6.2a. $\frac{a\sqrt{3}}{2}$.a= $\frac{a^{3}\sqrt{3}}{6}$Có AM là đường cao trong $\Delta $SAB vuông tại A => $\frac{1}{AM^{2}}$= $\frac{1}{AS^{2}}$+$\frac{1}{AB^{2}}$=> $AM^{2}$= $\frac{4a^{2}}{5}$=> $SM^{2}$= $\frac{16a^{2}}{5}$ => SM= $\frac{4a}{\sqrt{5}}$Tương t ự: SN= $\frac{4a}{\sqrt{5}}$Mà: SB=SC= a$\sqrt{5}$=> $\frac{SM}{SB} $=$\frac{SN}{SC}$=$\frac{4}{5}$=> $\frac{V_{SAMN}}{V_{SABC}}$= $\frac{SM}{SB} $.$\frac{SN}{SC}$=$\frac{16}{25}$$V_{SAMN}$ = $\frac{8\sqrt{3}.a^{3}}{75}$=> $V_{ABCNM}$= $V_{SABC}$- $V_{SAMN}$ = $\frac{3\sqrt{3}.a^{3}}{50}$
$V_{SABC}$= 1/3. SA.$S_{ABC}$= 1/6.2a. $\frac{a\sqrt{3}}{2}$.a= $\frac{a^{3}\sqrt{3}}{6}$Có AM là đường cao trong $\Delta $SAB vuông tại A => $\frac{1}{AM^{2}}$= $\frac{1}{AS^{2}}$+$\frac{1}{AB^{2}}$=> $AM^{2}$= $\frac{4a^{2}}{5}$=> $SM^{2}$= $\frac{16a^{2}}{5}$ => SM= $\frac{4a}{\sqrt{5}}$Tương t ự: SN= $\frac{4a}{\sqrt{5}}$Mà: SB=SC= a$\sqrt{5}$=> $\frac{SM}{SB} $=$\frac{SN}{SC}$=$\frac{4}{5}$=> $\frac{V_{SAMN}}{V_{SABC}}$= $\frac{SM}{SB} $.$\frac{SN}{SC}$=$\frac{16}{25}$$V_{SAMN}$ = $\frac{8\sqrt{3}.a^{3}}{75}$=> $V_{ABCNM}$= $V_{SABC}$- $V_{SAMN}$ = $\frac{3\sqrt{3}.a^{3}}{50}$
|
|
|
|
giải đáp
|
có bạn nào giúp mình k
|
|
|
|
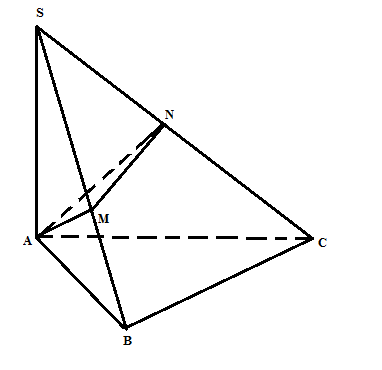 $V_{SABC}$= 1/3. SA.$S_{ABC}$= 1/6.2a. $\frac{a\sqrt{3}}{2}$.a= $\frac{a^{3}\sqrt{3}}{6}$ Có AM là đường cao trong $\Delta $SAB vuông tại A => $\frac{1}{AM^{2}}$= $\frac{1}{AS^{2}}$+$\frac{1}{AB^{2}}$=> $AM^{2}$= $\frac{4a^{2}}{5}$=> $SM^{2}$= $\frac{16a^{2}}{5}$ => SM= $\frac{4a}{\sqrt{5}}$ Tương t ự: SN= $\frac{4a}{\sqrt{5}}$ Mà: SB=SC= a$\sqrt{5}$ => $\frac{SM}{SB} $=$\frac{SN}{SC}$=$\frac{4}{5}$ => $\frac{V_{SAMN}}{V_{SABC}}$= $\frac{SM}{SB} $.$\frac{SN}{SC}$=$\frac{16}{25}$ $V_{SAMN}$ = $\frac{8\sqrt{3}.a^{3}}{75}$ => $V_{ABCNM}$= $V_{SABC}$- $V_{SAMN}$ = $\frac{3\sqrt{3}.a^{3}}{50}$ |
|
|
|
giải đáp
|
help me!!!
|
|
|
|
Các số
nguyên từ 1000 đến 9999 mà các chữ số của nó tăng dần từ trái sang
phải được hiểu là các số có 4 chữ số có dạng: $\overline{abcd}$sao cho các chữ
số a,b,c,d được chọn từ tập $\left\{ {1,2,3,4,5,6,7,8,9} \right\}$.
Chọn 4 chữ số bất kì trong 9 chữ số ta luôn được 1 cách sắp xếp sao
cho các chữ số của nó tăng dần từ trái sang phải. Như vậy số số
hạng thỏa mãn là: $C^{4}_{9}$=126 số
(Giải thích thêm: Chữ số 0
không được chọn do: số 0 đứng đầu sẽ thành số có 3 chữ số, chữ số
0 cũng không đứng ở các vị trí còn lại vì như vậy sẽ không thỏa
mãn giả thiết các chữ số tăng dần từ trái sang phải.) |
|
|
|
|
|
giải đáp
|
một bạn hỏi trên faceboook
|
|
|
|
$(1+2x+3x^{2})^{10}$= $((1+2x)+(3x^{2}))^{10}$
Khai triển có số hạng tổng quát là:
$C^{k}_{10}$ . $(1+2x)^{k}$. $(3x^{2})^{10-k}$= $C^{k}_{10}$ . $C^{n}_{k}$. $1^{k-n}$. $(2x)^{n}$. $(3x^{2})^{10-k}$= $C^{k}_{10}$ . $C^{n}_{k}$. $1^{k-n}$. $2^{n}$. $3^{10-k}$. $x^{20+n-2k}$
Với n, k thỏa mãn các điều kiện sau: k$\leqslant $10, n$\leqslant $k, 20+n-2k=3
=> (k,n)= $\left\{ {(9,1), (10,3)} \right\}$
Vậy hệ số của $x^{3}$ trong khai triển đa thức là: 540+960= 1500
|
|