|
|
sửa đổi
|
giúp mình bài hình
|
|
|
|
Gọi N là trung diểm của BC, gọi O là trọng tâm $\Delta$ABC. Từ O dựng OS vuông góc với mp (ABC)Trong mp (SAN) kẻ MG vuông góc với SN (1)Ta có: BC vuông góc vứoi ANBC vuông góc với SO=> BC vuông góc với (SAN) => BC vuông góc với MG (2)(1)(2) => MG vuông góc với mp(SBC) => MG= d(M, (SBC))Có: $\Delta$SNB vuông tại N=> $SN^{2}$ = $(2\sqrt{2})^{2}- a^{2}$Có: $\Delta$ ANB vuông tại N => tan A= $\frac{BN}{AN}$ => AN= a/$\sqrt{3}$Áp dụng hệ thức lượng với $\Delta$SAN: cosASN= $\frac{AS^{2}+SN^{2}-AN^{2}}{2.AS.SN}$= $\frac{4-\frac{a^{2}}{3}}{\sqrt{2}.\sqrt{8-a^{2}}}$ = cosMSG = $\frac{SG}{SM}$ => SG= $\frac{4-\frac{a^{2}}{3}}{\sqrt{2}.\sqrt{8-a^{2}}}$. $\sqrt{2}$= $\frac{4-\frac{a^{2}}{3}}{\sqrt{8-a^{2}}}$ Ta có: SGM là $\Delta$ vuô ngtại G => $MG^{2}$ = $SM^{2}-SG^{2}$= $\frac{a^{2}/9+ \frac{2a^{2}}{3}}{8- a^{2}}$ => MG= $\sqrt{\frac{a^{2}/9+ \frac{2a^{2}}{3}}{8- a^{2}}}$
Gọi N là trung diểm của BC, gọi O là trọng tâm $\Delta$ABC. Từ O dựng OS vuông góc với mp (ABC)Trong mp (SAN) kẻ MG vuông góc với SN (1)Ta có: BC vuông góc với ANBC vuông góc với SO=> BC vuông góc với (SAN) => BC vuông góc với MG (2)(1)(2) => MG vuông góc với mp(SBC) => MG= d(M, (SBC))Có: $\Delta$SNB vuông tại N=> $SN^{2}$ = $(2\sqrt{2})^{2}- a^{2}$Có: $\Delta$ ANB vuông tại N => tan A= $\frac{BN}{AN}$ => AN= a/$\sqrt{3}$Áp dụng hệ thức lượng với $\Delta$SAN: cosASN= $\frac{AS^{2}+SN^{2}-AN^{2}}{2.AS.SN}$= $\frac{4-\frac{a^{2}}{3}}{\sqrt{2}.\sqrt{8-a^{2}}}$ = cosMSG = $\frac{SG}{SM}$ => SG= $\frac{4-\frac{a^{2}}{3}}{\sqrt{2}.\sqrt{8-a^{2}}}$. $\sqrt{2}$= $\frac{4-\frac{a^{2}}{3}}{\sqrt{8-a^{2}}}$ Ta có: SGM là $\Delta$ vuô ngtại G => $MG^{2}$ = $SM^{2}-SG^{2}$= $\frac{a^{2}/9+ \frac{2a^{2}}{3}}{8- a^{2}}$ => MG= $\sqrt{\frac{a^{2}/9+ \frac{2a^{2}}{3}}{8- a^{2}}}$
|
|
|
|
sửa đổi
|
giúp mình bài hình
|
|
|
|
Gọi N là trung diểm của BC, gọi O là trọng tâm $\Delta$ABC. Từ O dựng OS vuông góc với mp (ABC)Trong mp (SAN) kẻ MG vuông góc với SN (1)Ta có: BC vuông góc vứoi ANBC vuông góc với SO=> BC vuông góc với (SAN) => BC vuông góc với MG (2)(1)(2) => MG vuông góc với mp(SBC) => MG= d(M, (SBC))Có: $\Delta$SNB vuông tại N=> $SN^{2}$ = $(2\sqrt{2})^{2}- a^{2}$Có: $\Delta$ ANB vuông tại N => tan A= $\frac{BN}{AN}$ => AN= a/$\sqrt{3}$Áp dụng hệ thức lượng với $\Delta$SAN: cosASN= $\frac{AS^{2}+SN^{2}-AN^{2}}{2.AS.SN}$= $\frac{4-\frac{a^{2}}{3}}{\sqrt{2}.\sqrt{8-a^{2}}}$ = cosMSG = $\frac{SG}{SM}$ => SG= $\frac{4-\frac{a^{2}}{3}}{\sqrt{2}.\sqrt{8-a^{2}}}$. $\sqrt{2}$= $\frac{4-\frac{a^{2}}{3}}{\sqrt{8-a^{2}}}$ Ta có: SGM là $\Delta$ vuô ngtại G => $MG^{2}$ = $SM^{2}-SG^{2}$= $\frac{a^{2}/9+ \frac{2a^{2}}{3}}{8- a^{2}}$ => MG= $\sqrt{\frac{a^{2}/9+ \frac{2a^{2}}{3}}{8- a^{2}}}$
Gọi N là trung diểm của BC, gọi O là trọng tâm $\Delta$ABC. Từ O dựng OS vuông góc với mp (ABC)Trong mp (SAN) kẻ MG vuông góc với SN (1)Ta có: BC vuông góc vứoi ANBC vuông góc với SO=> BC vuông góc với (SAN) => BC vuông góc với MG (2)(1)(2) => MG vuông góc với mp(SBC) => MG= d(M, (SBC))Có: $\Delta$SNB vuông tại N=> $SN^{2}$ = $(2\sqrt{2})^{2}- a^{2}$Có: $\Delta$ ANB vuông tại N => tan A= $\frac{BN}{AN}$ => AN= a/$\sqrt{3}$Áp dụng hệ thức lượng với $\Delta$SAN: cosASN= $\frac{AS^{2}+SN^{2}-AN^{2}}{2.AS.SN}$= $\frac{4-\frac{a^{2}}{3}}{\sqrt{2}.\sqrt{8-a^{2}}}$ = cosMSG = $\frac{SG}{SM}$ => SG= $\frac{4-\frac{a^{2}}{3}}{\sqrt{2}.\sqrt{8-a^{2}}}$. $\sqrt{2}$= $\frac{4-\frac{a^{2}}{3}}{\sqrt{8-a^{2}}}$ Ta có: SGM là $\Delta$ vuô ngtại G => $MG^{2}$ = $SM^{2}-SG^{2}$= $\frac{a^{2}/9+ \frac{2a^{2}}{3}}{8- a^{2}}$ => MG= $\sqrt{\frac{a^{2}/9+ \frac{2a^{2}}{3}}{8- a^{2}}}$
|
|
|
|
giải đáp
|
giúp mình bài hình
|
|
|
|
Gọi N là trung diểm của BC, gọi O là trọng tâm $\Delta$ABC. Từ O dựng OS vuông góc với mp (ABC)
Trong mp (SAN) kẻ MG vuông góc với SN (1)
Ta có: BC vuông góc với AN
BC vuông góc với SO
=> BC vuông góc với (SAN) => BC vuông góc với MG (2)
(1)(2) => MG vuông góc với mp(SBC) => MG= d(M, (SBC))
Có: $\Delta$SNB vuông tại N=> $SN^{2}$ = $(2\sqrt{2})^{2}- a^{2}$
Có: $\Delta$ ANB vuông tại N => tan A= $\frac{BN}{AN}$ => AN= a/$\sqrt{3}$
Áp dụng hệ thức lượng với $\Delta$SAN: cosASN= $\frac{AS^{2}+SN^{2}-AN^{2}}{2.AS.SN}$= $\frac{4-\frac{a^{2}}{3}}{\sqrt{2}.\sqrt{8-a^{2}}}$ = cosMSG = $\frac{SG}{SM}$
=> SG= $\frac{4-\frac{a^{2}}{3}}{\sqrt{2}.\sqrt{8-a^{2}}}$. $\sqrt{2}$= $\frac{4-\frac{a^{2}}{3}}{\sqrt{8-a^{2}}}$
Ta có: SGM là $\Delta$ vuô ngtại G => $MG^{2}$ = $SM^{2}-SG^{2}$= $\frac{a^{2}/9+ \frac{2a^{2}}{3}}{8- a^{2}}$
=> MG= $\sqrt{\frac{a^{2}/9+ \frac{2a^{2}}{3}}{8- a^{2}}}$
|
|
|
|
giải đáp
|
đếm số
|
|
|
|
Theo giả thiết, số tự nhiên có 3 chữ số mà chữ số đằng sau lớn hơn chữ số đằng trước hay số đằng trước lớn hơn chữ số đằng sau, chính là số tự nhiên có 3 chữ số đôi một khác nhau. Gọi số tự nhiên đó là: $\overline{abc}$ (a,b,c đôi một khác nhau)
Ta thấy: a có 9 cách chọn
b có 9 cách chọn
c có 8 cách chọn
=> Số các số tự nhiên thỏa mãn là: 9.9.8= 648 số
|
|
|
|
|
|
sửa đổi
|
Tích phân
|
|
|
|
=3/2. $\int\limits_{2}^{3}$$\frac{2x+6}{x^{2}-4x-5}$.dx= 3/2. $\int\limits_{2}^{3}$$\frac{(2x-4)+10}{x^{2}-4x-5}$.dx= 3/2. $\int\limits_{2}^{3}$$\frac{(x^{2}-4x-5)^{'}}{x^{2}-4x-5}$.dx + 15. $\int\limits_{2}^{3}$$\frac{1}{x^{2}-4x-5}$.dx = 3/2. $\ln \left| {x^{2}-4x-5} \right|$ ...+ 15. $\int\limits_{2}^{3}$$\frac{1}{(x-5)(x+1)}$.dx =3/2. $\ln \left| {x^{2}-4x-5} \right|$ ...+ 15. $\int\limits_{2}^{3}$$(\frac{1}{(x-5)}-\frac{1}{x+1})$.dx =3/2. $\ln \left| {x^{2}-4x-5} \right|$ ...+ 15. ($\ln \left| {x-5} \right|$- $\ln \left| {x+1} \right|$)... = 3/2 $\ln 8/9$+ 15$\ln 1/2$
=3/2. $\int\limits_{2}^{3}$$\frac{2x+6}{x^{2}-4x-5}$.dx= 3/2. $\int\limits_{2}^{3}$$\frac{(2x-4)+10}{x^{2}-4x-5}$.dx= 3/2. $\int\limits_{2}^{3}$$\frac{(x^{2}-4x-5)^{'}}{x^{2}-4x-5}$.dx + 15. $\int\limits_{2}^{3}$$\frac{1}{x^{2}-4x-5}$.dx = 3/2. $\ln \left| {x^{2}-4x-5} \right|$ + 15. $\int\limits_{2}^{3}$$\frac{1}{(x-5)(x+1)}$.dx =3/2. $\ln \left| {x^{2}-4x-5} \right|$ + 15. $\int\limits_{2}^{3}$$(\frac{1}{(x-5)}-\frac{1}{x+1})$.dx =3/2. $\ln \left| {x^{2}-4x-5} \right|$ + 15. ($\ln \left| {x-5} \right|$- $\ln \left| {x+1} \right|$) = 3/2 $\ln 8/9$+ 15$\ln 1/2$
|
|
|
|
giải đáp
|
Tích phân
|
|
|
|
=3/2. $\int\limits_{2}^{3}$$\frac{2x+6}{x^{2}-4x-5}$.dx= 3/2. $\int\limits_{2}^{3}$$\frac{(2x-4)+10}{x^{2}-4x-5}$.dx= 3/2. $\int\limits_{2}^{3}$$\frac{(x^{2}-4x-5)^{'}}{x^{2}-4x-5}$.dx + 15. $\int\limits_{2}^{3}$$\frac{1}{x^{2}-4x-5}$.dx = 3/2. $\ln \left| {x^{2}-4x-5} \right|$ 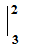 + 15. $\int\limits_{2}^{3}$$\frac{1}{(x-5)(x+1)}$.dx =3/2. $\ln \left| {x^{2}-4x-5} \right|$ 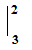 + 15. $\int\limits_{2}^{3}$$(\frac{1}{(x-5)}-\frac{1}{x+1})$.dx =3/2. $\ln \left| {x^{2}-4x-5} \right|$ 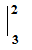 + 15. ($\ln \left| {x-5} \right|$- $\ln \left| {x+1} \right|$)  = 3/2 $\ln 8/9$+ 15$\ln 1/2$ |
|
|
|
giải đáp
|
gpt
|
|
|
|
Điều kiện xác định của bất phương trình là: 5- x>0 và 3-x>0 => x<3
Với điều kiện đó, do tính nghịch biến của hàm số logarit cơ số 1/3, bất phương trình tương đương với $\sqrt{5-x}$ > 3-x. Bởi vậy, ta có thể viết:
BPT<=> $\begin{cases}x<3 \\ \sqrt{5-x}>3-x \end{cases}$
<=>$\begin{cases}x<3 \\ 5-x> 9-6x+x^{2} \end{cases}$
<=> $\begin{cases}x<3 \\ x^{2}-5x+4<0 \end{cases}$
<=>$\begin{cases}x<3 \\ (x-1)(x-4)<0 \end{cases}$
<=>$\begin{cases}x<3 \\ 1<x<4 \end{cases}$
Vậy x$\in $(1;3)
|
|
|
|
sửa đổi
|
TOÁN 11
|
|
|
|
$\widehat{BAQ}$= $\widehat{NAC}$ (=$\widehat{BAC}$+ $90^{0}$)=> $\Delta$BAQ= $\Delta$NAC=> BQ= NC và $\widehat{ABQ}$= $\widehat{ANC}$Xét tứ giác MBON có: $\widehat{BON}$+ $\widehat{ONM}$+ $\widehat{NMB}$+ $\widehat{MBO}$= $\widehat{BON}$+ $\widehat{ONM}$+ $90^{0}$+ $90^{0}$+ $\widehat{ABQ}$= $\widehat{BON}$+ $90^{0}$+ $90^{0}$+ $\widehat{ONM}$+ $\widehat{ANC}$= $\widehat{BON}$+ $90^{0}$+ $90^{0}$+$90^{0}$= $360^{0}$ => $\widehat{BON}$= $90^{0}$ Vậy BQ vuôgn góc với NC.
$\widehat{BAQ}$= $\widehat{NAC}$ (=$\widehat{BAC}$+ $90^{0}$)=> $\Delta$BAQ= $\Delta$NAC=> BQ= NC và $\widehat{ABQ}$= $\widehat{ANC}$Xét tứ giác MBON có: $\widehat{BON}$+ $\widehat{ONM}$+ $\widehat{NMB}$+ $\widehat{MBO}$= $\widehat{BON}$+ $\widehat{ONM}$+ $90^{0}$+ $90^{0}$+ $\widehat{ABQ}$= $\widehat{BON}$+ $90^{0}$+ $90^{0}$+ $\widehat{ONM}$+ $\widehat{ANC}$= $\widehat{BON}$+ $90^{0}$+ $90^{0}$+$90^{0}$= $360^{0}$ => $\widehat{BON}$= $90^{0}$ Vậy BQ vuôgn góc với NC.
|
|
|
|
bình luận
|
TOÁN 11
Bài này trong " Nâng cao và một số chuyên đề 7 " có đấy bạn!
|
|
|
|
|
|
|
|
giải đáp
|
TOÁN 11
|
|
|
|
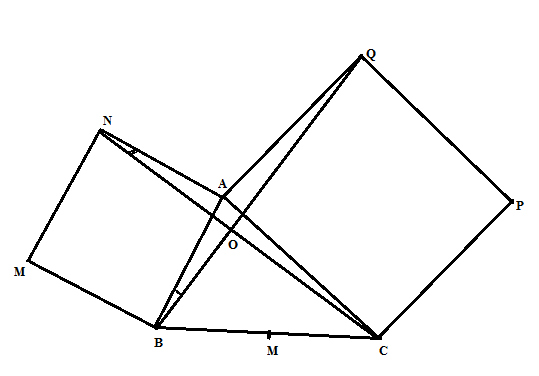 $\widehat{BAQ}$= $\widehat{NAC}$ (=$\widehat{BAC}$+ $90^{0}$) => $\Delta$BAQ= $\Delta$NAC => BQ= NC và $\widehat{ABQ}$= $\widehat{ANC}$ Xét tứ giác MBON có: $\widehat{BON}$+ $\widehat{ONM}$+ $\widehat{NMB}$+ $\widehat{MBO}$= $\widehat{BON}$+ $\widehat{ONM}$+ $90^{0}$+ $90^{0}$+ $\widehat{ABQ}$= $\widehat{BON}$+ $90^{0}$+ $90^{0}$+ $\widehat{ONM}$+ $\widehat{ANC}$= $\widehat{BON}$+ $90^{0}$+ $90^{0}$+$90^{0}$= $360^{0}$ => $\widehat{BON}$= $90^{0}$ Vậy BQ vuôgn góc với NC. |
|
|
|
sửa đổi
|
hình lăng trụ tam giác
|
|
|
|
Xét $\Delta$ AH$A_{1}$ vuông tại H => AH= A$A_{1}$. sin$30^{0}$= a/2=> $A_{1}H^{2}$= $a^{2}-a^{2}/4$= 3$a^{2}$/4 => $A_{1}H$= $\frac{a\sqrt{3}}{2}$Trong $\Delta$ đều $A_{1}B_{1}C_{1}$ cạnh a có $A_{1}H$= $\frac{a\sqrt{3}}{2}$ => H là trung điểm của $B_{1}C_{1}$=> $B_{1}C_{1}$ vuông góc với $A_{1}H$, mà AH vuông góc với $B_{1}C_{1}$ => $B_{1}C_{1}$ vuông góc với mp($A_{1}AH$) Trong mp($A_{1}AH$) kẻ HG vuông góc với $AA_{1}$ mà $B_{1}C_{1}$ vuông góc với mp($A_{1}AH$) => $B_{1}C_{1}$ vuông góc với HG=> HG là đoạn vuông góc chung của $AA_{1}$ và $B_{1}C_{1}$Xét $\Delta$ $HGA_{1}$ vuông tại G có HG= AH. sin $HA_{1}G$= $\frac{a\sqrt{3}}{2}$. sin 30= $\frac{a\sqrt{3}}{4}$
Xét $\Delta$ AH$A_{1}$ vuông tại H => AH= A$A_{1}$. sin$30^{0}$= a/2=> $A_{1}H^{2}$= $a^{2}-a^{2}/4$= 3$a^{2}$/4 => $A_{1}H$= $\frac{a\sqrt{3}}{2}$Trong $\Delta$ đều $A_{1}B_{1}C_{1}$ cạnh a có $A_{1}H$= $\frac{a\sqrt{3}}{2}$ => H là trung điểm của $B_{1}C_{1}$=> $B_{1}C_{1}$ vuông góc với $A_{1}H$, mà AH vuông góc với $B_{1}C_{1}$ => $B_{1}C_{1}$ vuông góc với mp($A_{1}AH$) Trong mp($A_{1}AH$) kẻ HG vuông góc với $AA_{1}$ mà $B_{1}C_{1}$ vuông góc với mp($A_{1}AH$) => $B_{1}C_{1}$ vuông góc với HG=> HG là đoạn vuông góc chung của $AA_{1}$ và $B_{1}C_{1}$Xét $\Delta$ $HGA_{1}$ vuông tại G có HG= AH. sin $HA_{1}G$= $\frac{a\sqrt{3}}{2}$. sin 30= $\frac{a\sqrt{3}}{4}$
|
|
|
|
giải đáp
|
hình lăng trụ tam giác
|
|
|
|
 Xét $\Delta$ AH$A_{1}$ vuông tại H => AH= A$A_{1}$. sin$30^{0}$= a/2 => $A_{1}H^{2}$= $a^{2}-a^{2}/4$= 3$a^{2}$/4 => $A_{1}H$= $\frac{a\sqrt{3}}{2}$ Trong $\Delta$ đều $A_{1}B_{1}C_{1}$ cạnh a có $A_{1}H$= $\frac{a\sqrt{3}}{2}$ => H là trung điểm của $B_{1}C_{1}$=> $B_{1}C_{1}$ vuông góc với $A_{1}H$, mà AH vuông góc với $B_{1}C_{1}$ => $B_{1}C_{1}$ vuông góc với mp($A_{1}AH$) Trong mp($A_{1}AH$) kẻ HG vuông góc với $AA_{1}$ mà $B_{1}C_{1}$ vuông góc với mp($A_{1}AH$) => $B_{1}C_{1}$ vuông góc với HG => HG là đoạn vuông góc chung của $AA_{1}$ và $B_{1}C_{1}$ Xét $\Delta$ $HGA_{1}$ vuông tại G có HG= AH. sin $HA_{1}G$= $\frac{a\sqrt{3}}{2}$. sin 30= $\frac{a\sqrt{3}}{4}$ |
|
|
|
|
|
bình luận
|
hình lăng trụ tam giác
Bài này không khó nhưng mình thấy lạ là giả thiết thừa nhiều quá, không cần những giả thiết đó mà mình vẫn tính được!
|
|
|
|
|
|