|
|
sửa đổi
|
bài thể tích khối chóp :((
|
|
|
|
Gọi O= AC$\cap $BDTrong mp(SAC) gọi G= AC'$\cap $SOTrong mp(SBD), từ G kẻ đường thẳng song song với BD cắt SB tại B', SD tại D'. Khi đó mp(P) chính là mp(AB'C'D') (Do BD song song với B'D' nên mp(P) song song với BD).Có G là trọng tâm $\Delta$SAC => $\frac{SG}{SO}$=$\frac{SB'}{SB}$=$\frac{SD'}{SD}$=$\frac{2}{3}$Ta có: $\frac{V_{S.AB'C'D'}}{V_{S.ABCD}}$=$\frac{V_{S.AB'C'}}{V_{S.ABC}}$+$\frac{V_{S.AC'D'}}{V_{S.ACD}}$ = $\frac{SB'}{SB}$. $\frac{SC'}{SC}$+ $\frac{SC'}{SC}$. $\frac{SD'}{SD}$ =2/3.1/2+1/2.2/3= 2/3Có ABCD là hình thoi, $\widehat{BAD}$= $60^{0}$ => $\Delta$ABD là tam giác đều cạnh a => $S_{ABCD}$=1/2.AC.BD= 1/2. a$\sqrt{3}$.a= $\frac{a^{2}.\sqrt{3}}{2}$=> $V_{S.ABCD}$= 1/3. SA. $S_{ABCD}$= $\frac{a^{3}.\sqrt{3}}{6}$=> $V_{S.AB'C'D'}$= $\frac{a^{3}.\sqrt{3}}{9}$
Gọi O= AC$\cap $BDTrong mp(SAC) gọi G= AC'$\cap $SOTrong mp(SBD), từ G kẻ đường thẳng song song với BD cắt SB tại B', SD tại D'. Khi đó mp(P) chính là mp(AB'C'D') (Do BD song song với B'D' nên mp(P) song song với BD).Có G là trọng tâm $\Delta$SAC => $\frac{SG}{SO}$=$\frac{SB'}{SB}$=$\frac{SD'}{SD}$=$\frac{2}{3}$Ta có: $\frac{V_{S.AB'C'D'}}{V_{S.ABCD}}$=$\frac{V_{S.AB'C'}}{V_{S.ABC}}$+$\frac{V_{S.AC'D'}}{V_{S.ACD}}$ = $\frac{SB'}{SB}$. $\frac{SC'}{SC}$+ $\frac{SC'}{SC}$. $\frac{SD'}{SD}$ =2/3.1/2+1/2.2/3= 2/3Có ABCD là hình thoi, $\widehat{BAD}$= $60^{0}$ => $\Delta$ABD là tam giác đều cạnh a => $S_{ABCD}$=1/2.AC.BD= 1/2. a$\sqrt{3}$.a= $\frac{a^{2}.\sqrt{3}}{2}$=> $V_{S.ABCD}$= 1/3. SA. $S_{ABCD}$= $\frac{a^{3}.\sqrt{3}}{6}$=> $V_{S.AB'C'D'}$= $\frac{a^{3}.\sqrt{3}}{9}$
|
|
|
|
sửa đổi
|
Tìm khoảng cách giúp mình với
|
|
|
|
Gọi G là trung điểm của DCĐồng nhất hình vẽ với hệ tọa độ không gian sao cho I trùng O, IB trùng Ox, IG trùng với Oy, IS trùng với OzKhi đó tọa độ các điểm là: I(0,0,0), A(-a/2,0,0), D(-a/2,-a,0), S(0,0,a$\sqrt{3}$/2), C(a/2,a,0)Ta có $\overrightarrow{AS}$= (a/2,0,a$\sqrt{3}$/2)= (1,0,$\sqrt{3}$)$\overrightarrow{AD}$=(0,-a,0)= (0,1,0)=> Vector pháp tuyến của mp(ASD)= $\left[ {\overrightarrow{AS}.\overrightarrow{AD}} \right]$= ($\sqrt{3}$,0,-1)=> Phương trình mp(ASD) là: $\sqrt{3}$x- z+ $\frac{\sqrt{3}a}{2}$=0=> d(C, (SAD))= $\frac{4\sqrt{3}a}{19}$
Gọi G là trung điểm của DCĐồng nhất hình vẽ với hệ tọa độ không gian sao cho I trùng O, IB trùng Ox, IG trùng với Oy, IS trùng với OzKhi đó tọa độ các điểm là: I(0,0,0), A(-a/2,0,0), D(-a/2,-a,0), S(0,0,a$\sqrt{3}$/2), C(a/2,a,0)Ta có $\overrightarrow{AS}$= (a/2,0,a$\sqrt{3}$/2)= (1,0,$\sqrt{3}$)$\overrightarrow{AD}$=(0,-a,0)= (0,1,0)=> Vector pháp tuyến của mp(ASD)= $\left[ {\overrightarrow{AS}.\overrightarrow{AD}} \right]$= ($\sqrt{3}$,0,-1)=> Phương trình mp(ASD) là: $\sqrt{3}$x- z+ $\frac{\sqrt{3}a}{2}$=0=> d(C, (SAD))= $\frac{4\sqrt{3}a}{19}$
|
|
|
|
giải đáp
|
bài thể tích khối chóp :((
|
|
|
|
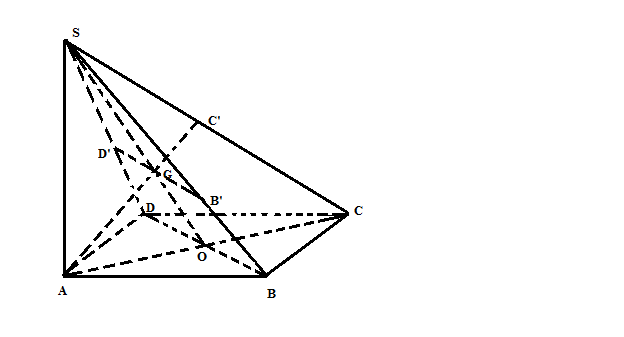 Gọi O= AC$\cap $BD Trong mp(SAC) gọi G= AC'$\cap $SO Trong mp(SBD), từ G kẻ đường thẳng song song với BD cắt SB tại B', SD tại D'. Khi đó mp(P) chính là mp(AB'C'D') (Do BD song song với B'D' nên mp(P) song song với BD). Có G là trọng tâm $\Delta$SAC => $\frac{SG}{SO}$=$\frac{SB'}{SB}$=$\frac{SD'}{SD}$=$\frac{2}{3}$ Ta có: $\frac{V_{S.AB'C'D'}}{V_{S.ABCD}}$=$\frac{V_{S.AB'C'}}{V_{S.ABC}}$+$\frac{V_{S.AC'D'}}{V_{S.ACD}}$ = $\frac{SB'}{SB}$. $\frac{SC'}{SC}$+ $\frac{SC'}{SC}$. $\frac{SD'}{SD}$ =2/3.1/2+1/2.2/3= 2/3 Có ABCD là hình thoi, $\widehat{BAD}$= $60^{0}$ => $\Delta$ABD là tam giác đều cạnh a => $S_{ABCD}$=1/2.AC.BD= 1/2. a$\sqrt{3}$.a= $\frac{a^{2}.\sqrt{3}}{2}$ => $V_{S.ABCD}$= 1/3. SA. $S_{ABCD}$= $\frac{a^{3}.\sqrt{3}}{6}$ => $V_{S.AB'C'D'}$= $\frac{a^{3}.\sqrt{3}}{9}$ |
|
|
|
giải đáp
|
Tìm khoảng cách giúp mình với
|
|
|
|
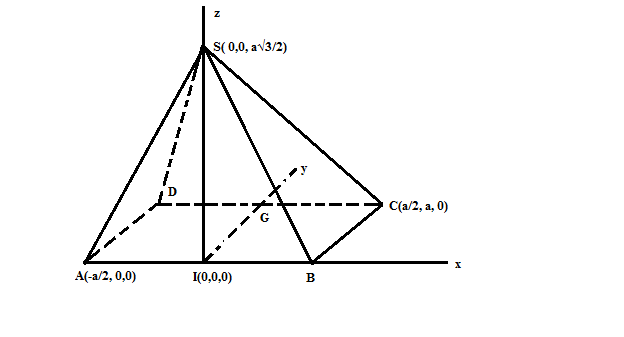 Gọi G là trung điểm của DC Đồng nhất hình vẽ với hệ tọa độ không gian sao cho I trùng O, IB trùng Ox, IG trùng với Oy, IS trùng với Oz Khi đó tọa độ các điểm là: I(0,0,0), A(-a/2,0,0), D(-a/2,-a,0), S(0,0,a$\sqrt{3}$/2), C(a/2,a,0) Ta có $\overrightarrow{AS}$= (a/2,0,a$\sqrt{3}$/2)= (1,0,$\sqrt{3}$) $\overrightarrow{AD}$=(0,-a,0)= (0,1,0) => Vector pháp tuyến của mp(ASD)= $\left[ {\overrightarrow{AS}.\overrightarrow{AD}} \right]$= ($\sqrt{3}$,0,-1) => Phương trình mp(ASD) là: $\sqrt{3}$x- z+ $\frac{\sqrt{3}a}{2}$=0 => d(C, (SAD))= $\frac{4\sqrt{3}a}{19}$ |
|
|
|
giải đáp
|
làm bài thống kê cho vui nào ?
|
|
|
|
Gọi X là số giày dép bán ra trong một ngày.
Số giày bán ($X_{i}$) 17 18 19 20 21 22 23 24 25 26
Tần suất ($m_{i}$) 1 2 4 5 3 4 3 3 1 1
a/ Số giày dép trung bình bán ra trong ngày: $\overline{X}$=$\frac{1}{n}$.$\sum_{i=1}^{k}$$m_{i}x_{i}$= $\frac{17.1+18.2+19.4+20.5+21.3+22.4+23.3+24.3+25.1+26.1}{30}$=19.67
Vậy số giày dép bán ra trung bình là 20 đôi
c/ Phương sai: $s^{2}$= $\frac{1}{n}$.$\sum_{i=1}^{k}$$m_{i}x_{i}^{2}$- $\overline{X}^{2}$ = 1/3O. ($17^{2}$.1+$18^{2}$.2+$19^{2}$.4+$20^{2}$.5+$21^{2}$.3+$22^{2}$.4+$23^{2}$.3+$24^{2}$.3+$25^{2}$.1+$26^{2}$.1)- $19.67^{2}$= 21.62
Độ lệch chuẩn: $s= \sqrt{s^{2}}$= 4.65
|
|
|
|
giải đáp
|
Bài này nữa
|
|
|
|
Đồng nhất hình vẽ với hệ trục toạn độ trong không gian sao cho A' $\Xi$O, A'B' $\Xi$Ox, A'D'$\Xi$ Oy, A'A$\Xi$Oz
Khi đó, tọa độ các điểm là: A'(0,0,0), D(0,a,a), C( a,a,a), K(0,a,a/2)
Theo công thức tính khoảng cách 2 đường chéo nhau trong không gian tọa dộ. Ta có:
d( A'D, CK)=$\frac{\left| {\left[ {\overrightarrow{A'D},\overrightarrow{CK}} \right].\overrightarrow{KD}} \right|}{\left| {\left[ {\overrightarrow{A'D},\overrightarrow{CK}} \right]} \right|}$
Mà $\overrightarrow{A'D}$=(0,a,a); $\overrightarrow{CK}$=( -a,0,-a/2); $\overrightarrow{KD}$=(0,0,-a/2)
=> d(A'D, CK)=$\frac{a}{3}$
|
|
|
|
giải đáp
|
Bài toán chọn số học sinh từ một lớp thỏa các điều kiện.
|
|
|
|
c/ Chọn 5 người tùy ý có: $C^{5}_{40}$ cách
Những cách chọn không thỏa mãn là:
+ 0 nữ, 5 nam thì có: $C^{5}_{25}$ cách
+ 1 nữ, 4 nam thì có: $C^{1}_{15}$.$C^{4}_{25}$
=> Số cách chọn thỏa mãn là: $C^{5}_{40}$- $C^{5}_{25}$- $C^{1}_{15}$.$C^{4}_{25}$
d/ Tổ trưởng là nữ có: $C^{1}_{15}$ cách chọn bạn tổ trưởng. Đây là 1 biến độc lập với biến còn lại
Số cách chọn 4 bạn còn lại là: $C^{1}_{15}$.$C^{3}_{25}$ + $C^{2}_{15}$.$C^{2}_{25}$ +$C^{3}_{15}$.$C^{1}_{25}$ + $C^{4}_{15}$.$C^{0}_{25}$
Vậy số cách chọn thỏa mãn là: $C^{1}_{15}$.$C^{1}_{15}$.$C^{3}_{25}$ + $C^{1}_{15}$. $C^{2}_{15}$.$C^{2}_{25}$ +$C^{1}_{15}$.$C^{3}_{15}$.$C^{1}_{25}$ + $C^{1}_{15}$. $C^{4}_{15}$.$C^{0}_{25}$
C425C5C52CC425
|
|
|
|
giải đáp
|
Bài toán chọn số học sinh từ đội văn nghệ.
|
|
|
|
Chọn 8 người trong 15 người có $C^{8}_{15}$
Những cách chọn không thỏa mãn là:
0 nữ, 8 nam thì có: $C^{8}_{10}$
1 nữ, 7 nam thì có: $C^{1}_{5}$.$C^{7}_{10}$
2 nữ, 6 nam thì có: $C^{2}_{5}$.$C^{6}_{10}$
Vậy số cách chọn thỏa mãn là: C815 -C810-C 15.C710C71- C25.C610= 3690C610
|
|
|
|
sửa đổi
|
Bài toán về hình chóp với thiết diện.
|
|
|
|
Trong mp(ABCD) gọi G =MN$\cap $BD, H= MN$\cap $AC. Khi đó, mp(PMN) trở thành mp(PNH) Vì P, G $\in $ mp(SBD), xét trong mp(SBD) gọi Q= PG$\cap $SDVì H, P $\in $ mp(SAC), trong mp(SAC), gọi X = HP $\cap $ SA, J = HP $\cap $ SCKhi đó, thiết diện của (MNP) với hình chóp là mp (MNJQX)P/s: giả thiết bài cho chưa tốt vì thừa dữ kiện mà vẫn giải được, giả thiết ABCD là hình bình hành chưa được sử dụng. Hình bình hành cần cho kẻ các mối quan hệ song song, trong bài này thì không cho cái tỉ lệ nào bằng nhau cả, nên khi tìm thiết diện chỉ dùng quan hệ giao nhau!
Trong mp(ABCD) gọi G =MN$\cap $BD, H= MN$\cap $AC. Khi đó, mp(PMN) trở thành mp(PNH) Vì P, G $\in $ mp(SBD), xét trong mp(SBD) gọi Q= PG$\cap $SDVì H, P $\in $ mp(SAC), trong mp(SAC), gọi X = HP $\cap $ SA, J = HP $\cap $ SCKhi đó, thiết diện của (MNP) với hình chóp là mp (MNJQX)P/s: giả thiết bài cho chưa tốt vì thừa dữ kiện mà vẫn giải được, giả thiết ABCD là hình bình hành chưa được sử dụng. Hình bình hành cần cho kẻ các mối quan hệ song song, trong bài này thì không cho cái tỉ lệ nào bằng nhau cả, nên khi tìm thiết diện chỉ dùng quan hệ giao nhau!
|
|
|
|
giải đáp
|
Bài toán về hình chóp với thiết diện.
|
|
|
|
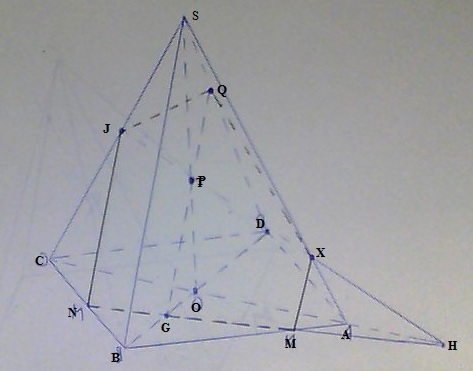 Trong mp(ABCD) gọi G =MN$\cap $BD, H= MN$\cap $AC. Khi đó, mp(PMN) trở thành mp(PNH) Vì P, G $\in $ mp(SBD), xét trong mp(SBD) gọi Q= PG$\cap $SD Vì H, P $\in $ mp(SAC), trong mp(SAC), gọi X = HP $\cap $ SA, J = HP $\cap $ SC Khi đó, thiết diện của (MNP) với hình chóp là mp (MNJQX) P/s: giả thiết bài cho chưa tốt vì thừa dữ kiện mà vẫn giải được, giả thiết ABCD là hình bình hành chưa được sử dụng. Hình bình hành cần cho kẻ các mối quan hệ song song, trong bài này thì không cho cái tỉ lệ nào bằng nhau cả, nên khi tìm thiết diện chỉ dùng quan hệ giao nhau! |
|
|
|
|
|
giải đáp
|
Tính khoảng cách giúp mình với mọi người ơi
|
|
|
|
b/ mp$(CB'D') // BD$ do $ BD// B'D'$
gọi $I=AC$$\cap $BD,$ I'=A'C'$$\cap $B'D'
Trong $mp(ACC'A')$ kẻ$ IN(N\in CI')$ vuông góc với $CI'$
Mặt khác,$ B'D'$ vuông góc với mp $(ACC'A') =>B'D'$ vuông góc với$IN => IN $vuông góc với mp$( CB'D') $chứa $CB'$
Vậy $IN$ chính là đường vuông góc chung giữa $BD$ và $CB'$
$a/ d(BC', CD') = d(BD,CB') =IN$
Xét $\Delta INC$ đồng dạng với $\Delta I'IC$ (góc-góc)$ \Rightarrow IN//II'= IC //CI'$
Có$ II'=AA'=a$
$IC=\frac{1}{2} CA= \frac{a \sqrt{2} }{2} $
$CI'=\sqrt{CC'^2 +I'C'^2}=\frac{a \sqrt{3} }{2} $
$\Rightarrow IN=\frac{a \sqrt{2} }{\sqrt{3} } $
Vậy $d(BC', CD')=\frac{a \sqrt{2} }{\sqrt{3} } $
|
|
|
|
|
|
|
|
bình luận
|
hình giải tích
Đây là lời giải đúng, lời giải dưới bị sai!
|
|
|
|
|
|