\(2x^{2}+2\left(m+1\right)x
+m^{2}+4m+3=0\)
a/
\(\Delta’=m^{2}+2m+1-2\left(m^{2} +4m+3\right)= -m^{2}-6m-5\)
Để
phương trình có nghiệm thì \( \Delta’ \geq 0\)
\(\Leftrightarrow -m^{2}-6m-5 \geq 0 \)
$\Leftrightarrow m^{2}+6m+5 \leq 0 \Leftrightarrow -5 \leq m \leq -1 (*) $
b/
Với điều kiện \( (*)\), phương trình có hai nghiệm:
\(
x_{1}= \frac{ -\left(m+1\right) -\sqrt{ -\left(m^{2}+6m+5\right)}}{2};
x_{2}=\frac{-\left(m+1\right)+\sqrt{ -\left(m^{2}+6m+5\right)}}{2}\) hiển nhiên \( x_{1} <x_{2} \).
Để
phương trình có ít nhất một nghiệm lớn
hơn \(1\) thì:
\(
1<x_{2} \Leftrightarrow \frac{-\left(m+1\right)+\sqrt{ -\left(m^{2}+6m+5\right)} }{2} \) hiển nhiên \( x_{1} <x_{2}>1 \)
\(
\Leftrightarrow -\left(m+1\right)+ sqrt{ -\left(m^{2}+6m+5\right)}>2\)
\(
\Leftrightarrow \sqrt{-\left(m^{2}+6m+5\right)} < m+3 (*’) \)
+/
Nếu \( -5<m\leq -3 (*’) \) luôn đúng
+/
Nếu \( -3<m<-1\): bình phương hai vế:
\(
-m^{2}-6m-5> m^{2}+6m+9\)
$\Leftrightarrow 2m^{2} +12m +14 <0 \Leftrightarrow m^{2}+6m+7<0 \Leftrightarrow -3-\sqrt{2}<m< -3+\sqrt{2}$
Giao
với $ -3<m<-1$ được $-3<m<-3+\sqrt{2}$
\(1<x_{1}
\Leftarrow 1< \frac{ -\left(m+1\right) -\sqrt{ -\left(m^{2}+6m+5\right)}}{2}\)
\(\Leftrightarrow
2< -\left(m+1\right) -\sqrt{ -\left(m^{2}+6m+5\right)}\)
\(\Leftrightarrow
\sqrt{ -\left(m^{2}+6m+5\right)}< -\left(m+3\right)\)
Nếu
\( -5<m<-3\): Bình phương hai vế:
\(-m^{2}-6m-5<
m^{2}+6m+9\)
\(
2m^{2}+12m+14>0 \Leftrightarrow m^{2}+6m+7>0 \Leftrightarrow m< -3-\sqrt{2}
\) hay \( m> -3+\sqrt{2}\)
Giao
với \(-5<m<-3\) được \(-5<m<-3-\sqrt{2} \)
Vậy
để phương trình có ít nhất một nghiệm lớn hơn \(1\) thì \( m\in \left( -5;
-3-\sqrt{2}\right) \) hoặc \( m \in \left( -3; -3+\sqrt{2} \right)\)
c/
Từ phương trình: \(2x^{2}+2\left(m+1\right)x +m^{2}+4m+3=0\), với \(m\in[ -5;
-1] \), phương trình có hai nghiệm \( x_{1}, x_{2} \) và
\(
x_{1}+x_{2}=-\left( m+1\right), x_{1}x_{2}=\frac{m^{2}+4m+3}{2}\)
\(
A=| x_{1}x_{2}-2\left(x_{1}+x_{2}\right)|\)
\(
= |\frac{m^{2}+4m+3}{2}+2\left( m+1\right)| \)
\(=
| \frac{m^{2}+8m+7}{2}|\)
Xem
đồ thị hàm số \( y=| \frac{m^{2}+8m+7}{2}|
\) trên \( [ -5; -1] \)
Đồ
thị \( y=| \frac{m^{2}+8m+7}{2}| \) trên \( [ -5; -1] \) là phần nét đậm.
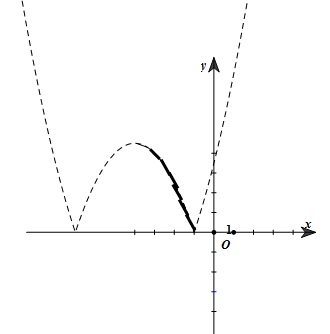
Từ
đồ thị \( \Leftarrow \) giá trị lớn nhất của biểu thức A là \( 4,5\) đạt được
khi \( m=-4\)