|
|
$\begin{array}{l}
(1) \Leftrightarrow {\log _3}\left[ {m{x^2} - \left( {{m^2} + 1} \right)x + m} \right] \ge {\log
_3}\left( { - {x^2} - x + {m^2} + m} \right)\\
\Leftrightarrow m{x^2} - \left( {{m^2} + 1} \right)x + m \ge - {x^2} - x + {m^2} + m\\
\ \Leftrightarrow \left\{ \begin{array}{l}
m{x^2} - \left( {{m^2} + 1} \right)x + m > 0\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,(2)\\
- {x^2} - x + {m^2} + m \ge 0\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,(3)
\end{array} \right.
\end{array}$
$f(x) = - {x^2} - x + {m^2} + m$có $2$ nghiệm $x = m,\,\,\,x = - m - 1$
$g(x) = m{x^2} - \left( {{m^2} + 1} \right)x + m$ với $m = - 1$ có 1 nghiệm $x = - 1$
Với $m \ne - 1$ có 2 nghiệm $\,\,\,\,\,x = m,\,\,\,x = - \frac{m}{{m + 1}}$
Khi $m = - 1$ thì hệ ($2), (3$) trở thành : $\left\{ \begin{array}{l}
- {x^2} - x > 0\\
- x - 1 \ge 0
\end{array} \right.$hệ này vô nghiệm.
Khi $m \ne - 1\,\,\,:$ để có nghiệm của hệ ($2),(3$) ta cần so sánh $3$ số: $m,\,\,\, - m -
1,\,\,\frac{{ - m}}{{m + 1}}$
xét dấu các hiệu : $m - \left( { - m - 1} \right) = 2m + 1;$
$m - \left( {\frac{{ - m}}{{m + 1}}} \right) = \frac{{{m^2} + 2m}}{{m + 1}};\,\,\,\,\,\frac{{ -
m}}{{m + 1}} - \left( { - m - 1} \right) = \frac{{{m^2} + m + 1}}{{m + 1}}$
Bảng xét dấu:
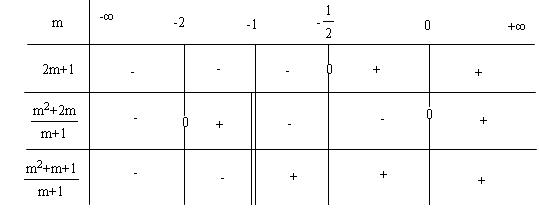
Ta có các trường hợp sau:
$a)\,\,m \le - 2:\,\,\,$do$ - \frac{m}{{m + 1}} < - m - 1$ nên hệ có nghiệm là:
$m < x < - \frac{m}{{m + 1}}$
$b)\,\, - 2 < m < - 1:\,\,\left\{ \begin{array}{l}
m < x < - m - 1\\
\frac{{ - m}}{{m + 1}} \le x \le m
\end{array} \right.$ vô nghiệm
$c)\,\, - 1 < m < - \frac{1}{2}:\,\,\,\left\{ \begin{array}{l}
m < x < - m - 1\\
x \le m\,\,\,;\,\,\,x > \frac{{ - m}}{{m + 1}}
\end{array} \right.$ vô nghiệm
$d)\,\, - \frac{1}{2} \le m < 0:\,\,\left\{ \begin{array}{l}
- m - 1 < x < m\\
x \le m\,\,\,;\,\,\,x > \frac{{ - m}}{{m + 1}}
\end{array} \right.$
Hệ có nghiệm là:$ - m - 1 < x < m$
$e)\,\,\,\,\,\,\,\,\,\left\{ \begin{array}{l}
- m - 1 < x < m\\
x \le \frac{{ - m}}{{m + 1}};\,\,\,x \ge m
\end{array} \right.$
$ \Rightarrow
$ Hệ có nghiệm là $ - m - 1 < x \le \frac{{ - m}}{{m + 1}}$
|