|
|
Tập xác định $R$.
${y^ / } = 1 - {e^{ - x}}$ điểm cực tiểu $\left\{ \begin{array}{l}
x = 0\\
{y_{CT}} = 1
\end{array} \right.$
${y^{ / / }} = {e^{ - x}} > 0$ hàm số lõm trên $R$
$\mathop {\lim \,}\limits_{x \to + \infty } y = + \infty \,\,\,,\,\,\,\mathop {\lim \,}\limits_{x
\to - \infty } \left( {x + {e^{ - x}}} \right) = \mathop {\lim \,}\limits_{x \to + \infty } x\left( {1 -
\frac{{{e^{ - x}}}}{{{e^{ - x}}}}} \right) = \left( { - \infty } \right)\left( { - \infty } \right) = +
\infty $
$\mathop {\lim \,}\limits_{x \to + \infty } \left( {y - x} \right) = \mathop {\lim \,}\limits_{x
\to + \infty } {e^{ - x}} = 0\,\,\,\, \Rightarrow $ đường thẳng $y = x$là đường tiệm cận xiên.
Bảng biến thiên:
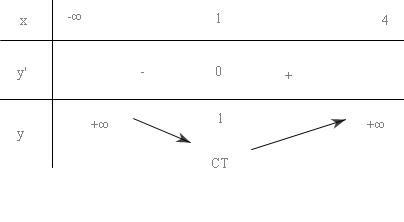
Đồ thị :
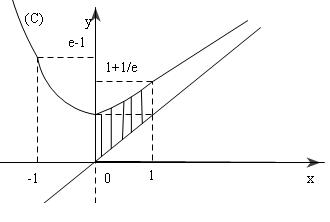
Diện tích: $S = \int\limits_0^1 {\left[ {\left( {x + {e^{ - x}}} \right) - x} \right]} dx =
\int\limits_0^1 {{e^{ - x}}dx} $
$S = - \left. {{e^{ - x}}} \right]_0^1 = 1 - \frac{1}{e}\,\,\,\,$đvtt
|