$1.$ $I=\frac{-1}{3}\int\limits^1_0
x^3(1-x^3)^6d(1-x^3)$
Đặt $
t=1-x^3\Rightarrow I=-\frac{1}{3}\int\limits^1_0
(1-t)t^6dt=\frac{-1}{3}(\frac{t^7}{7}-\frac{t^8}{8})|^1_0=\frac{-1}{168}$
$2.$
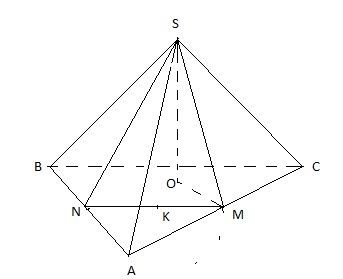
Do $\Delta ABC$ đều, $M,N$ là trung điểm của $AC,AB$ nên $AM=AN=\frac{AB}{2}=\sqrt{6} $
$dt AMN=\frac{1}{2} AM.AN.sin60^0=\frac{3\sqrt{3} }{2} $.
Vậy $V_{SAMN}=\frac{1}{3} .\frac{3\sqrt{3} }{2}.1=\frac{\sqrt{3} }{2} $
- Giả sử $O_1$ là tâm hình cầu nội tiếp hình chóp $SAMN$ và $r$ là bán kính hình cầu thì $r$ chính là độ dài các đường cao các hình chóp đỉnh $O_1$ và đáy là các mặt tứ diện $SAMN.$ Như vậy :
$V_{SAMN}=\frac{1}{3} r(dtAMN+dtASM+dtASN+dtSMN (*)$
Do hình chóp $SAMN $đều nên chân đường cao $O$ trùng với tâm dường tròn nội tiếp $\Delta ABC$ suy ra $OM\bot AC,ON\bot AB$ và $OS\bot (ABC)$
$\Rightarrow SM\bot AC,SN\bot AB\Rightarrow SM=SN$
Xét $\Delta AOM$ có $OM=AM.tan30^0=\sqrt{2} $
$\Rightarrow OM=ON=\sqrt{2} $.
Xét $\Delta SOM$ có $SM=\sqrt{OM^2+SO^2}=\sqrt{2+1}=\sqrt{3} $
$\Rightarrow dtASM=\frac{1}{2} AM.SM=\frac{1}{2} \sqrt{6}.\sqrt{3}=\frac{3\sqrt{2} }{2} $
Tương tự $dtASN=\frac{3\sqrt{2} }{2} $.Giả sử $K$ là trung điểm $MN$ thì $SK\bot MN $(do $\Delta SMN$ cân)
Xét $\Delta SKM$ có $SK=\sqrt{SM^2-KM^2}=\sqrt{3-\frac{3}{2} } =\frac{\sqrt{6} }{2} $
$\Rightarrow dtSMN=\frac{1}{2} MN.SK=\frac{1}{2} \sqrt{6}.\frac{1}{2} \sqrt{6} =\frac{3}{2} $ Thay vào $*$
$\Rightarrow \frac{\sqrt{3} }{2} =\frac{1}{3} r(\frac{3\sqrt{3} }{2}+\frac{3\sqrt{2} }{2}+\frac{3\sqrt{2} }{2}+\frac{3}{2} )$
$r=\frac{\sqrt{3} }{1+2\sqrt{2} +\sqrt{3} } $