Dễ chứng minh công thức $l_a=\frac{2bc}{(b+c)} .cos\frac{A}{2}(1) $ (sử dụng phương pháp diện tích)
$\Leftrightarrow l_a.\frac{b+c}{bc}=2cos\frac{A}{2} \Rightarrow l_a(\frac{1}{b}+\frac{1}{c} )=2cos\frac{A}{2} $
$\Rightarrow l_a(\frac{1}{b} +\frac{1}{c} )+l_b(\frac{1}{c} +\frac{1}{a} )+l_c(\frac{1}{a} +\frac{1}{b} )=2(cos\frac{A}{2}+cos\frac{B}{2}+cos\frac{C}{2} )$
$\Rightarrow \frac{1}{c} (l_a+l_b)+\frac{1}{b} (l_a+l_c)+\frac{1}{a} (l_b+l_c)=2(cos\frac{A}{2}+cos\frac{B}{2}+cos\frac{C}{2} )$
Cũng dễ chứng minh được rằng nếu $x,y,z$ là $3$ góc nhọn thì
$cosx+cosy+cosz\leq 3.cos\frac{x+y+z}{3}(2) $
$\Rightarrow cos\frac{A}{2}+cos\frac{B}{2}+cos\frac{C}{2} \leq 3cos\frac{A+B+C}{6} =\frac{3\sqrt{3} }{2} $
$\Rightarrow\frac{1}{c} (l_a+l_b)+\frac{1}{b} (l_a+l_c)+\frac{1}{a} (l_b+l_c)\leq 3\sqrt{3} $
Đẳng thức xảy ra $\Leftrightarrow \Delta ABC$ đều
(
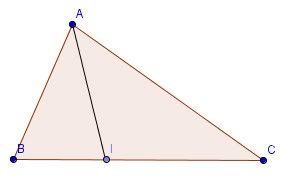
Chứng minh (1):
$S_{ABC}=S_{ABI}+S_{ACI}\Leftrightarrow bc\sin
A=cl_a\sin\frac{A}{2}+bl_a\sin\frac{A}{2}$
$\Leftrightarrow l_a=\frac{2bc\cos\frac{A}{2}}{b+c}$
Chứng minh (2):
Đặt
$f(t)=\cos t, t\in(0;\frac{\pi}{2})$
$\Rightarrow
f’(t)=-\sin t; f’’(t)=-\cos t<0, \forall t\in(0;\frac{\pi}{2})$
Theo
BĐT Jensen :
$f(x)+f(y)+f(z)\leq
3f(\frac{x+y+z}{3})\Rightarrow (2)$