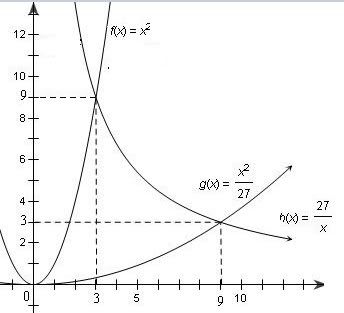
Xét các PT giao điểm :
$x^2=\frac{x^2}{27}\Leftrightarrow x=0$
$x^2=\frac{27}{x}\Leftrightarrow x=3$
$\frac{x^2}{27}=\frac{27}{x}\Leftrightarrow x=9$
$S=\int\limits_{0}^{3}(x^2-\frac{x^2}{27} ) dx+\int\limits_{3}^{9} (\frac{27}{x} -\frac{x^2}{27} )$
$=\frac{26}{27} .\frac{x^3}{3} \mathop |\nolimits_0^3 +27lnx\mathop |\nolimits_3^9 -\frac{1}{27} .\frac{x^3}{3} \mathop |\nolimits_3^9 =27ln3$ (đvdt)