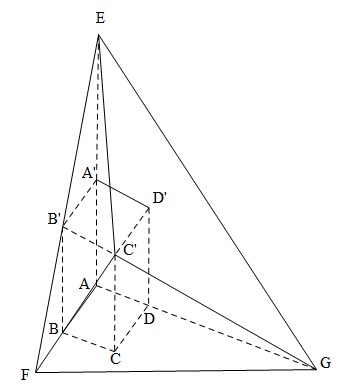
a)Ta có:
$V_{AEFG}=V_{C'AFG}+V_{C'AEG}+V_{C'AEF}$
$\Rightarrow \frac{V_{C'AFG}}{V}+\frac{V_{C'AEG}}{V}+\frac{V_{C'AEF}}{V}=1 (1)$
(Vì: $V=V_{AEFG}$)
Mà: $\begin{cases}V=\frac{1}{6}AE.AF.AG \\ V_{C'AFG}= \frac{1}{6}a.AF.AG \\V_{C'AEG}=\frac{1}{6}b.AE.AG \\V_{C'AEF}=\frac{1}{6}c.AE.AF \end{cases}$
Thay vào $(1)$ $\Rightarrow \frac{a}{AE}+\frac{b}{AF}+\frac{c}{AG}=1$
$\Rightarrow$ (ĐPCM)
b)Áp dụng BĐT Cauchy:
$1=\frac{a}{AE}+\frac{b}{AF}+\frac{c}{AG}\geq 3\sqrt[3]{\frac{abc}{AE.AF.AG}}$
$\Rightarrow AE.AF.AG\geq 27abc$
$\Rightarrow V=\frac{1}{6}AE.AF.AG\geq \frac{9}{2}abc$
Dấu "=" xảy ra $\Leftrightarrow \frac{a}{AE}=\frac{b}{AF}=\frac{c}{AG}=\frac{1}{3}$
$\Leftrightarrow \begin{cases}AE=3a\\ AF=3b \\ AG=3c \end{cases}$
Vậy: $\min(V)= \frac{9}{2}abc$