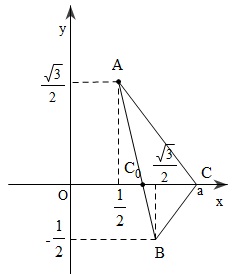
Trong mặt phẳng $Oxy$,chọn $A(\frac{1}{2},\frac{\sqrt{3}}{2});B(\frac{\sqrt{3}}{2},-\frac{1}{2});C(a,0)$
Lúc đó: $\begin{cases} CA=\sqrt{(a-\frac{1}{2})^{2}+\frac{3}{4}}=\sqrt{a^{2}-a+1}\\CB=\sqrt{(a-\frac{\sqrt{3}}{2})^{2}+\frac{1}{4}}=\sqrt{a^{2}-\sqrt{3}a+1}\\AB=\sqrt{(\frac{\sqrt{3}}{2}-\frac{1}{2})^{2}+(\frac{\sqrt{3}}{2}+\frac{1}{2})^{2}}=\sqrt{2} \end{cases}$
Trong $\triangle ABC: CA+CB\geq AB$
$\Leftrightarrow \sqrt{a^{2}-a+1}+\sqrt{a^{2}-\sqrt{3}a+1}\geq \sqrt{2}$.
Dấu "=" xảy ra $\Leftrightarrow \overrightarrow{CA}//\overrightarrow{CB}$
$\Leftrightarrow a-\frac{1}{2}=\sqrt{3}(\frac{\sqrt{3}}{2}-a)$
$\Rightarrow a(\sqrt{3}+1)=2 \Rightarrow a=\frac{2}{1+\sqrt{3}}=\sqrt{3}-1$