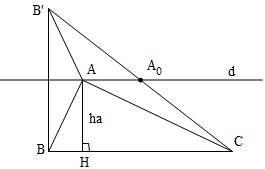
Gọi $d$ là đường thẳng qua $A$ và $//BC$.
$B'$ là điểm đối xứng của $B$ qua $d \Rightarrow BB'=2h_a$.
Ta có: $AC+AB=AC+AB'\geq B'C=\sqrt{B'B^2+BC^2}$
$\Rightarrow b+c\geq \sqrt{a^{2}+4h_{a}^{2}}$
$\Rightarrow (b+c)^{2}\geq a^{2}+4h_{a}^{2}$
$\Rightarrow 4h_{a}^{2}\leq (b+c)^{2}- a^{2}=(b+c+a)(b+c-a)$
$\Rightarrow 4h_{a}^{2}\leq 2p.2(p-a)$
$\Rightarrow h_{a}\leq \sqrt{p(p-a)}$
Dấu "=" xảy ra $\Leftrightarrow A\equiv A_{0} \Leftrightarrow b=c$
$\Rightarrow$ (ĐPCM)