Bài 107365

Question

Cho

$\triangle ABC$ có

$a,b,c$ là độ dài các cạnh.

Chứng minh rằng:

$a^{2}b(a-b)+b^{2}c(b-c)+c^{2}a(c-a)\geq 0$

score 0 · Answer 1

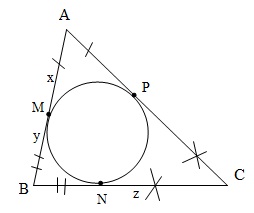
Dựng đường tròn nội tiếp

$\triangle ABC$ .

Đặt:

$\begin{cases} AM=x\\ BM=y\\ CN=z \end{cases}$

Khi đó:

$\begin{cases} a=y+z\\ b=z+x\\ c=x+y \end{cases}$

BĐT cần chứng minh:

$\Leftrightarrow (y+z)^{2}(z+x)(y-x)+(z+x)^{2}(x+y)(z-y)+(x+y)^{2}(y+z)(x-z)\geq 0$

$\Leftrightarrow y^{3}z+z^{3}x+x^{3}y\geq xyz(x+y+z)$

$\Leftrightarrow \frac{y^{2}}{x}+\frac{z^{2}}{y}+\frac{x^{2}}{z}\geq x+y+z (*)$

Cách

$1:$ Theo BĐT Bunhiacopski:

$(x+y+z)^{2}=(\frac{y}{\sqrt{x}}.\sqrt{x}+\frac{z}{\sqrt{y}}.\sqrt{y}+\frac{x}{\sqrt{z}}.\sqrt{z})^{2}\leq (\frac{y^{2}}{x}+\frac{z^{2}}{y}+\frac{x^{2}}{z})(x+y+z)$

$\Rightarrow \frac{y^{2}}{x}+\frac{z^{2}}{y}+\frac{x^{2}}{z} \geq x+y+z$
Cách

$2:$ Theo BĐT Cosy:

$\frac{y^2}x+x\ge 2y; \frac{z^2}y+y\ge 2z; \frac{x^2}z+z\ge 2x$
Cộng

$3$ bất đẳng thức trên vế theo vế ta được:

$\frac{y^2}x+x+\frac{z^2}y+y+\frac{x^2}z+z\ge 2(x+y+z) \Leftrightarrow \frac{y^{2}}{x}+\frac{z^{2}}{y}+\frac{x^{2}}{z} \geq x+y+z$

$\Rightarrow (*)$ đúng.

$\Rightarrow$ (ĐPCM)

Bài 107365

1 Đáp án

Lý thuyết liên quan

Bài 107365

1 Đáp án

Liên quan

Lý thuyết liên quan