|
|
1. Định nghĩa
Cho một điểm $O$ cố định và một số k không đổi, $k \ne 0$. Phép biến hình mỗi điểm $M$ thành điểm $M’$ sao cho $\overrightarrow {OM'} = k\overrightarrow {OM} $ được gọi là phép vị tự tâm $O$ tỷ số $k$.
2. Các tính chất của phép vị tự
ĐỊNH LÝ 1
Nếu phép vị tự tỉ số k biến hai điểm M và N lần lượt thành hai điểm M’ và N’ thì
$\overrightarrow {M'N'} = k\overrightarrow {MN} $ và $M'N' = \left| k \right|MN$.
ĐỊNH LÝ 2
Phép vị tự biến ba điểm thẳng hàng thành ba điểm thẳng hàng và không làm thay đổi thứ tự của ba điểm thẳng hàng đó.
HỆ QUẢ
Phép vị tự tỷ số k biến đường thẳng thành đường thẳng song song (hoặc trùng) với đường thẳng đó, biến tia thành tia, biến đoạn thẳng thành đoạn thẳng mà độ dài được nhân lên với $\left| k \right|$, biến tam giác thành tam giác đồng dạng với tỷ số đồng dạng là $\left| k \right|$, biến góc thành góc bằng nó.
3. Ảnh của đường tròn qua phép vị tự
ĐỊNH LÝ 3
Phép vị tự tỷ số k biến đường tròn có bán kính R thành đường tròn có bán kính $\left| k \right|R$.
4. Tâm vị tự của hai đường tròn
Ta đã biết rằng phép vị tự biến đường tròn thành đường tròn. Bây giờ ta xét bài toán ngược lại.
Thuật ngữ:
Nếu có phép vị tự tâm O biến đường tròn này thành đường tròn kia thì O được gọi là tâm vị tự của hai đường tròn đó
Nếu phép vị tự đó có tỉ số dương thì điểm O được gọi là tâm vị tự ngoài, nếu phép vị tự đó có tỉ số âm thì O được gọi là tâm vị tự trong
5. Ứng dụng của phép vị tự
Bài toán 2
Tam giác ABC có hai đỉnh B, C cố định còn đỉnh A chạy trên một đường tròn$\left( {O;R} \right)$ cố định không có điểm chung với đường thẳng BC. Tìm quỹ tích trọng tâm G của tam giác ABC.
Giải
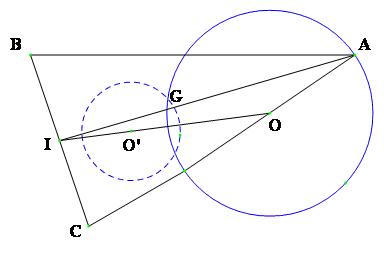
Gọi I là trung điểm của BC thì I cố định. Điểm G là trọng tâm tam giác ABC khi và chỉ khi $\overrightarrow {IG} = \frac{1}{3}\overrightarrow {IA} $
Như vậy phép vị tự V tâm I tỷ số $\frac{1}{3}$ biến điểm A thành điểm G. Từ đó suy ra khi A chạy trên đường tròn $\left( {O;R} \right)$ thì quỹ tích G là ảnh của đường tròn đó qua phép vị tự V, tức là đường tròn $\left( {O';R'} \right)$ mà $\overrightarrow {IO'} = \frac{1}{3}\overrightarrow {IO} $ và $R' = \frac{1}{3}R$
|