|
|
1, Vị trí tương đối giữa đường thẳng và mặt phẳng
Cho một đường thẳng a và một mặt phẳng $\left( P \right)$. Ta thấy có ba trường hợp sau đây sảy ra:
a, Đường thẳng a và $mp\left( P \right)$ có hai điểm chung phân biệt. Khi đó, theo định lý ở bài 1, đường thẳng a nằm trên $mp\left( P \right)$, tức là $a \subset mp\left( P \right)$
b, Đường thẳng a và $mp\left( P \right)$ có một điểm chung duy nhất A. Khi đó ta nói a và $\left( P \right)$cắt nhau tại A và viết $a \cap \left( P \right) = \left\{ A \right\}$hoặc $a \cap \left( P \right) = A$
c, Đường thẳng a và $mp\left( P \right)$ không có điểm chung nào cả. Khi đó ta nói rằng đường thẳng a song song với $mp\left( P \right)$, hoặc $mp\left( P \right)$ song song với đường thẳng a, hoặc a và $\left( P \right)$song song với nhau, và viết $a\parallel \left( P \right)$hoặc $\left( P \right)\parallel a$
ĐỊNH NGHĨA
Một đường thẳng và một mặt phẳng gọi là song song với nhau nếu chúng không có điểm chung
2. Điều kiện để một đường thẳng song song với một mặt phẳng
ĐỊNH LÝ 1
Nếu đường thẳng a không nằm trên mặt phẳng $\left( P \right)$ và song song với một đường thẳng nào đó nằm trên $\left( P \right)$ thì a song song với $\left( P \right)$
3. Tính chất
ĐỊNH LÝ 2
Nếu đường thẳng a song song với mặt phẳng$\left( P \right)$ thì mọi mặt phẳng$\left( Q \right)$ chứa a mà cắt $\left( P \right)$ thì cắt theo giao tuyến song song với a
HỆ QUẢ 1
Nếu một đường thẳng song song với một mặt phẳng thì nó song song với một đường thẳng nào đó trong mặt phẳng.
HỆ QUẢ 2
Nếu hai mặt phẳng cắt nhau cùng song song với một đường thẳng thì giao tuyến của chúng cũng song song với đường thẳng đó
ĐỊNH LÝ 3
Nếu a và b là hai đường thẳng chéo nhau thì có duy nhất một mặt phẳng chứa a và song song với b
Ví dụ
Cho tứ diện ABCD. Gọi M là một điểm nằm trên cạnh AB (M khác A và B). Giả sử $\left( P \right)$ là mặt phẳng qua M song song với các đường thẳng AC và BD. Hãy xác định thiết diện của hình tứ diện ABCD khi cắt bởi mặt phẳng$\left( P \right)$. Thiết diện là hình gì?
Giải
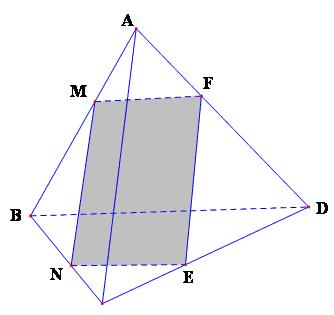
Từ M kẻ đường thẳng song song với AC cắt BC tại N và kẻ đường thẳng song song với BD cắt AD tại F. Khi ấy, $\left( P \right)$ chính là $mp\left( {MNF} \right)$. Gọi E là giao điểm của$\left( P \right)$ với CD thì thiết diện là tứ giác MNEF. Vì đường thẳng MN song song với $mp\left( {ACD} \right)$ nên $mp\left( P \right)$ qua MN cắt $mp\left( {ACD} \right)$theo giao tuyến EF song song với MN. Tương tự, NE song song với MF. Vậy thiết diện cần tìm là hình bình hành MNEF.
|