|
|
1. Vị trí tương đối của hai mặt phẳng phân biệt
Khi cho hai mặt phẳng phân biệt $\left( P \right)$và $\left( Q \right)$, có thể xảy ra một trong hai trường hợp sau đây:
A, $\left( P \right)$và $\left( Q \right)$ có điểm chung. Khi đó ta biết rằng $\left( P \right)$và $\left( Q \right)$cắt nhau theo một đường thẳng
B, $\left( P \right)$và $\left( Q \right)$không có điểm chung. Trong trường hợp này, ta nói chúng song song với nhau (hoặc song song)
ĐỊNH NGHĨA
Hai mặt phẳng gọi là song song với nhau nếu chúng không có điểm chung.
2. Điều kiện để hai mặt phẳng song song
ĐỊNH LÝ 1
Nếu mặt phẳng $\left( P \right)$ chứa hai đường thẳng a, b cắt nhau và cùng song song với mặt phẳng $\left( Q \right)$ thì $\left( P \right)$song song với$\left( Q \right)$
3. Tính chất
TÍNH CHẤT 1
Qua một điểm nằm ngoài một mặt phẳng, có một và chỉ một mặt phẳng song song với mặt phẳng đó
HỆ QUẢ 1
Nếu đường thẳng a song song với mặt phẳng $\left( Q \right)$thì có duy nhất một mặt phẳng $\left( P \right)$chứa a và song song với $\left( Q \right)$
HỆ QUẢ 2
Hai mặt phẳng phân biệt cùng song song với mặt phẳng thứ 3 thì song song với nhau
TÍNH CHẤT 2
Nếu hai mặt phẳng $\left( P \right)$và $\left( Q \right)$song song thì mọi mặt phẳng $\left( R \right)$đã cắt $\left( P \right)$thì phải cắt $\left( Q \right)$và các giao tuyến của chúng song song.
4. Định lý Talet trong không gian
ĐỊNH LÝ 2
Ba mặt phẳng đôi một song song chắn ra trên hai cát tuyến bất kỳ các đoạn thẳng tương ứng tỉ lệ
Ta thừa nhận định lý sau đây, gọi là Định lý đảo
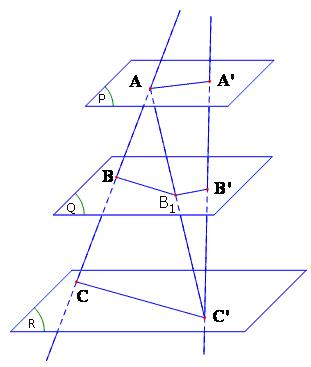
Cho hai đường thẳng chéo nhau a và a’. Lấy các điểm phân biệt A, B, C trên a và A’, B’, C’ trên a’ sao cho
$\frac{{AB}}{{A'B'}} = \frac{{BC}}{{B'C'}} = \frac{{CA}}{{C'A'}}$
Khi đó, ba đường thẳng AA’, BB’, CC’ lần lượt nằm trên ba mặt phẳng song song, tức là chúng cùng song song với một mặt phẳng
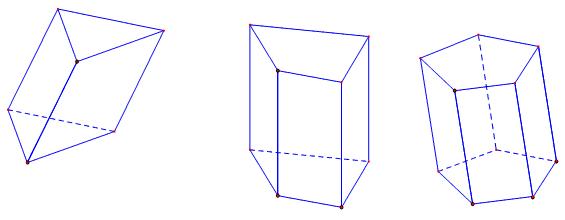
5. Hình lăng trụ và hình hộp
ĐỊNH NGHĨA HÌNH LĂNG TRỤ
Hình hợp bởi các hình bình hành ${A_1}{A_2}A{'_2}A{'_1},\,\,\,\,{A_2}{A_3}A{'_3}A{'_2},\,\,\,...,\,{A_n}{A_1}A{'_1}A{'_n}$ và hai đa giác${A_1}{A_2}...{A_n},\,\,\,\,A{'_1}A{'_2}...A{'_n}$gọi là hình lăng trụ hay lăng trụ, và kí hiệu là ${A_1}{A_2}...{A_n}.A{'_1}A{'_2}...A{'_n}$
Mỗi hình bình hành nói trên gọi là mặt bên của lăng trụ. Hai đa giác ${A_1}{A_2}...{A_n},\,\,\,\,A{'_1}A{'_2}...A{'_n}$ gọi là 2 mặt đáy của lăng trụ. Các cạnh của 2 đa giác đó gọi là các cạnh đáy; các đoạn thẳng ${A_1}A{'_1},{A_2}A{'_2},...,{A_n}A{'_n}$ gọi là các cạnh bên của lăng trụ. Các đỉnh của 2 mặt đáy gọi là các đỉnh của lăng trụ
Nếu đáy của lăng trụ là tam giác, tứ giác, ngũ giác thì lăng trụ tương ứng gọi là lăng trụ tam giác, lăng trụ tứ giác, lăng trụ ngũ giác
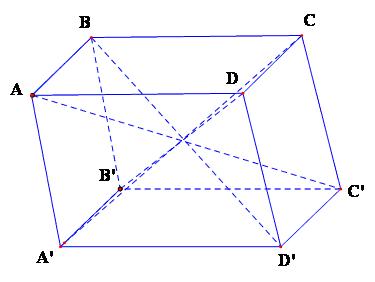
Sau đây ta sẽ giới thiệu một dạng đặc biệt của hình lăng trụ, đó là hình hộp
Hình lăng trụ có đáy là hình bình hành được gọi là hình hộp
Như vậy, hình hộp có sáu mặt (bốn mặt bên và hai mặt đáy) đều là những hình bình hành. Mỗi mặt có một mặt song song với nó. Hai mặt như thế gọi là hai mặt đối diện.
6. Hình chóp cụt
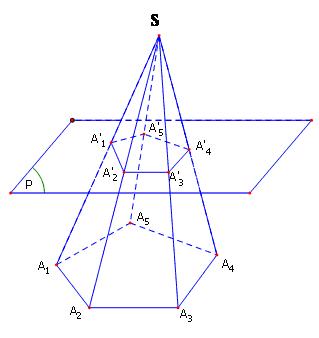
ĐỊNH NGHĨA
Cho hình chóp $S.{A_1}{A_2}...{A_n}$và một mặt phẳng $\left( P \right)$không qua đỉnh, song song với mặt phẳng đáy, cắt các cạnh $S{A_1},\,S{A_2},\,...,S{A_n}$ lần lượt tại $A{'_1},\,A{'_2},...,A{'_n}$. Hình hợp bởi thiết diện $A{'_1}A{'_2}...A{'_n}$và đáy${A_1}{A_2}...{A_n}$của hình chóp cùng với các tứ giác $A{'_1}A{'_2}{A_2}{A_1}$,$A{'_2}A{'_3}{A_3}{A_2}$, $A{'_n}A{'_1}{A_1}{A_n}$gọi là một hình chóp cụt, kí hiệu là $A{'_1}A{'_2}...A{'_n}.{A_1}{A_2}...{A_n}$( Hình 72 trang 66)
Đáy của hình chóp gọi là đáy lớn của hình chóp cụt, còn thiết diện $A{'_1}A{'_2}...A{'_n}$gọi là đáy nhỏ của hình chóp cụt. Các tứ giác$A{'_1}A{'_2}{A_2}{A_1}$,$A{'_2}A{'_3}{A_3}{A_2}$,$A{'_n}A{'_1}{A_1}{A_n}$gọi là các mặt bên của hình chóp cụt. Các đoạn thẳng, ${A_1}A{'_1}$,${A_2}A{'_2}$,…,${A_n}A{'_n}$gọi là các cạnh bên của hình chóp cụt.
Tùy theo đáy là tam giác, tứ giác, ngũ giác,…, ta có hình chóp cụt tam giác, hình chóp cụt tứ giác, hình chóp cụt ngũ giác,…
TÍNH CHẤT
Vì hình chóp cụt được cắt ra từ một hình chóp nên ta dễ dàng suy ra tính chất sau đây
Hình chóp cụt có:
a, Hai đáy là hai đa giác có cạnh tương ứng song song và tỉ số các cạnh tương ứng bằng nhau.
b, Các mặt bên là những hình thang
c, Các đường thẳng chứa các cạnh bên đồng quy tại một điểm.
|