|
|
giải đáp
|
Đường thẳng vuông góc với mặt phẳng(2).
|
|
|
|
d/ Có $\Delta$SHA= $\Delta$SKA (C.G.C)
=> SH=SK
=> $\frac{SH}{SB}=\frac{SK}{SD}$
=> HK//BD
Theo phần b: BD vuông góc với (SAC)
=> HK vuông góc với (SAC)
+ BD vuông góc với (SAC)=> BD vuông góc với AI, mà BD// HK
=> HK vuông góc với AI ( ĐPCM)
|
|
|
|
giải đáp
|
Đường thẳng vuông góc với mặt phẳng(2).
|
|
|
|
c/ Theo cm ở câu a: BC vuông góc với (SAB) => BC vuông góc với AH, mà AH lại vuông góc với SB => AH vuông góc với (SBC) => AH vuông góc với SC (1)
Theo cm ở câu a: DC vuông góc với (SAD) => DC vuông góc với AK, mà AK lại vuông góc với SD => AK vuông góc với (SDC) => AK vuông góc với SC (2)
Mặt khác theo giả thiết AI vuông góc với SC (3)
(1)(2)(3) => SC vuông góc với 3 đường thẳng AH, AI, AK => AH, AI, AK đồng phẳng (đpcm)
|
|
|
|
|
|
giải đáp
|
Đường thẳng vuông góc với mặt phẳng(2).
|
|
|
|
a/ 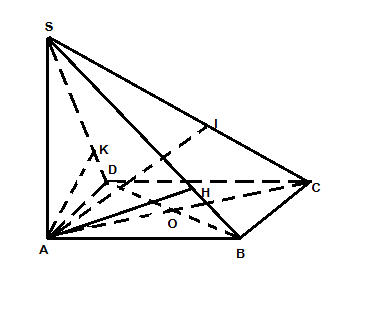 SA vuông góc với đáy => SA vuông góc với AB, AD => SAB, SAD là những tam giác vuông SA cũng vuông góc với BC mà BC vuông góc với AB => BC vuông góc với (SAB) => BC vuông góc với SB => SBC là tam giác vuông SA cũng vuông góc với DC mà DC vuông góc với AD => DC vuông góc với (SAD) => DC vuông góc với SD => SDC là tam giác vuông (ĐPCM) |
|
|
|
bình luận
|
Đường thẳng vuông góc với mặt phẳng(5).
Bạn xem lại câu b giúp mình nhé. Sao lại "Đường thẳng qua A vuông góc với SC cắt BC,CD lần lượt tại I,J;H là hình chiếu vuông góc của A lên SC." Chỗ này có gì nhầm lẫn không :)
|
|
|
|
|
|
|
|
sửa đổi
|
Đường thẳng vuông góc với mặt phẳng(5).
|
|
|
|
a/ Chú ý: câu a là câu gợi ý cho ta cách vẽ hình!Có: CD vuông góc với SD, CD vuông góc với DA => CD vuông góc với (SAD) => CD vuông góc với SA (1) CB vuông góc với SB, CB vuông góc với BA => CB vuông góc với (SAB) => CB vuông góc với SA (2)(1)(2)=> SA vuông góc với mp(ABCD)+ Tính SA Có: $SC^{2}=SD^{2}+DC^{2}$ => $SC^{2}=6a^{2}$$AC^{2}=AB^{2}+BC^{2}$ => $AC^{2}=4a^{2}$Mà $SC^{2}=SA^{2}+AC^{2}$ => $SA^{2}=2a^{2}$ => SA= a$\sqrt{2}$
a/ Chú ý: câu a là câu gợi ý cho ta cách vẽ hình!Có: CD vuông góc với SD, CD vuông góc với DA => CD vuông góc với (SAD) => CD vuông góc với SA (1) CB vuông góc với SB, CB vuông góc với BA => CB vuông góc với (SAB) => CB vuông góc với SA (2)(1)(2)=> SA vuông góc với mp(ABCD)+ Tính SA Có: $SC^{2}=SD^{2}+DC^{2}$ => $SC^{2}=6a^{2}$$AC^{2}=AB^{2}+BC^{2}$ => $AC^{2}=4a^{2}$Mà $SC^{2}=SA^{2}+AC^{2}$ => $SA^{2}=2a^{2}$ => SA= a$\sqrt{2}$
|
|
|
|
giải đáp
|
Đường thẳng vuông góc với mặt phẳng(5).
|
|
|
|
a/ Chú ý: câu a là câu gợi ý cho ta cách vẽ hình! 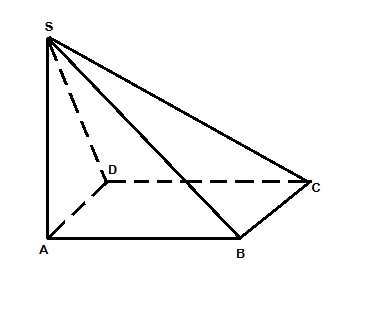 Có: CD vuông góc với SD, CD vuông góc với DA => CD vuông góc với (SAD) => CD vuông góc với SA (1) CB vuông góc với SB, CB vuông góc với BA => CB vuông góc với (SAB) => CB vuông góc với SA (2) (1)(2)=> SA vuông góc với mp(ABCD) + Tính SA Có: $SC^{2}=SD^{2}+DC^{2}$ => $SC^{2}=6a^{2}$ $AC^{2}=AB^{2}+BC^{2}$ => $AC^{2}=4a^{2}$ Mà $SC^{2}=SA^{2}+AC^{2}$ => $SA^{2}=2a^{2}$ => SA= a$\sqrt{2}$ |
|
|
|
giải đáp
|
toán hình học 11
|
|
|
|
Lời giải này có yêu cầu trả vỏ sò để xem. Bạn hãy link trên để vào xem chi tiết
|
|
|
|
giải đáp
|
toán hình học 11
|
|
|
|
2/ Vì EMNF là hình thang vuông nên: $S_{EMNF}$= 1/2. (EM+EN). EF (1) +Có EM là đường trung bình trong tam giác SAB => EM= 1/2AB= a (2) + Tính FN: 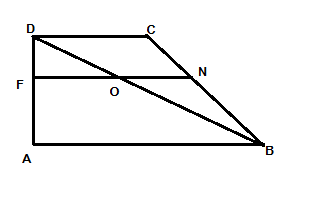 Có: $\frac{FO}{AB}=\frac{DF}{DA}=\frac{x}{a}$ => FO= 2x Có: $\frac{ON}{DC}=\frac{BN}{BC}=\frac{AF}{AD}=\frac{a-x}{a}$ => ON= a-x => FN= a+x (3) + Có: $EF^{2}=EA^{2}+AF^{2}=a^{2}+x^{2}$ => EF= $\sqrt{a^{2}+x^{2}}$ (4) (1)(2)(3)(4) => $S_{EMNF}$= 1/2. (2a+x). $\sqrt{a^{2}+x^{2}}$ |
|
|
|
đặt câu hỏi
|
Giúp mình với. Thanks!
|
|
|
|
Cho A là ma trận vuông cấp n có dạng:
A= ($a_{ij}$) , $a_{ij}$= i+j, i,j= 1,2,.........,n
Tính hạng của ma trận A?
|
|
|
|
đặt câu hỏi
|
Giúp mình với!
|
|
|
|
Cho ma trận
A= $\begin{pmatrix}2 & -1&0&0\\ 0 & 2&-1&0\\ 0&0&2&-1\\ 0&0&0&2\end{pmatrix}$
Tìm tất cả các ma trận thực vuông X cấp 4 sao cho AX= XA
|
|
|
|
|
|
sửa đổi
|
Áp dụng BĐT Bernoulli
|
|
|
|
Bằng cách đổi biến nọ kia ta có thể giả sử a=b=c=1như thế thì x^{2} +y^{2}=1Trường hợp 1 : n chẵn = 2k . Ta sẽ tạo điểm rơi cho các bdt Cauchy như sau d.x^{2k}+u+u+...+u \geq k . \sqrt[k]{d.u^{k-1}} . x^{2} ( gồm k-1 số u )e.y^{2k}+v+v+...+v \geq k . \sqrt[k]{e.v^{k-1}} . y^{2} ( gồm k-1 số v )Để có thể áp dụng được giả thiết thì d. u^{k-1}=e. v^{k-1} Từ đẳng thức này ta tính được \frac{u}{v}=\sqrt[k-1]{\frac{e}{d}} (1)mà khi xảy ra dấu bằng thì d.x^{2k}=u , e.y^{2k}= v (2)Từ 1 và 2 ta sẽ tìm được giá trị của x và y , từ đó tìm được u và v , suy ra được minVì là bài tổng quát nên em sẽ không đi chi tiết vào kết quả , chị có thể chọn d=1 , e=3 , n = 6 để minh họaTrường hợp 2 : n=2k+1Tương tự như trường hợp 1 nhưng sẽ áp dụng như thế nàyd.x^{2k+1} +d. x^{2k+1}+ u +u+......+u gồm 2k-1 số u e.y^{2k+1} +d. y^{2k+1}+ v +v+......+v gồm 2k-1 số vMặc dù có vẻ phức tạp nhưng trong những trường hợp riêng thì khá đơn giản
Bằng cách đổi biến nọ kia ta có thể giả sử a=b=c=1như thế thì $x^{2} +y^{2}=1$Trường hợp 1 : n chẵn = 2k . Ta sẽ tạo điểm rơi cho các bdt Cauchy như sau $d.x^{2k}+u+u+...+u \geq k . \sqrt[k]{d.u^{k-1}} . x^{2}$ ( gồm k-1 số u )$e.y^{2k}+v+v+...+v \geq k . \sqrt[k]{e.v^{k-1}} . y^{2}$ ( gồm k-1 số v )Để có thể áp dụng được giả thiết thì $d. u^{k-1}=e. v^{k-1}$ Từ đẳng thức này ta tính được $\frac{u}{v}=\sqrt[k-1]{\frac{e}{d}}$ (1)mà khi xảy ra dấu bằng thì $d.x^{2k}=u , e.y^{2k}= v$ (2)Từ 1 và 2 ta sẽ tìm được giá trị của x và y , từ đó tìm được u và v , suy ra được minVì là bài tổng quát nên em sẽ không đi chi tiết vào kết quả , chị có thể chọn d=1 , e=3 , n = 6 để minh họaTrường hợp 2 : n=2k+1Tương tự như trường hợp 1 nhưng sẽ áp dụng như thế này$d.x^{2k+1} +d. x^{2k+1}+ u +u+......+u$ gồm 2k-1 số u $e.y^{2k+1} +d. y^{2k+1}+ v +v+......+v$ gồm 2k-1 số vMặc dù có vẻ phức tạp nhưng trong những trường hợp riêng thì khá đơn giản
|
|
|
|
đặt câu hỏi
|
Áp dụng BĐT Bernoulli
|
|
|
|
Gỉa sử: x,y>0 thỏa mãn: $a.x^{2}+b.y^{2}=c$ (a,b,c>0)
Tìm Min M= $d.x^{n}+e.y^{n}$
a,b,c,d,e tùy chọn
|
|
|
|
giải đáp
|
Giup e bai nay
|
|
|
|
Lời giải này có yêu cầu trả vỏ sò để xem. Bạn hãy link trên để vào xem chi tiết
|
|