|
|
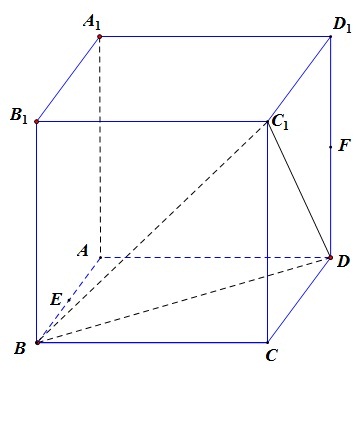
Chọn hệ trục tọa độ trực chuẩn $Axyz$ sao cho \(B\left( {2,0,0} \right);D\left( {0,2,0} \right);{A_1}\left( {0,0,2} \right)\). Như vậy
\(E\left( {1,0,0} \right);F\left( {0,2,1} \right);{C_1}\left( {2,2,2} \right)\)
$1$.
\(\overrightarrow {BD} \left( { - 2,2,0} \right); \overrightarrow {D{C_1}} \left( {2,0,2} \right)\); \(\left[ {\overrightarrow {BD} ,\overrightarrow {D{C_1}} } \right] = \left( {4,4, - 4} \right)\)
Mặt phẳng \(\left( {BD{C_1}} \right)\) có vecto pháp tuyến là \(\overrightarrow v = \left( {1,1, - 1} \right)\), do đó có phương trình \(x + y - z - 2 = 0 \left( 1 \right)\)
Dễ thấy $E(1, 0, 0)$ có tọa độ không thỏa mãn $(1)$ \( \Rightarrow E \notin \left( {B{C_1}D} \right)\)
Mà
\(\overrightarrow {{\rm{E}}F} = \left( { - 1,2,1} \right);\overrightarrow {{\rm{E}}F} .\overrightarrow v = - 1 + 2.1 + \left( { - 1} \right).1 = 0 \Rightarrow \overrightarrow {{\rm{E}}F} \bot \overrightarrow v \\ \Rightarrow {\rm{E}}F//\left( {BD{C_1}} \right);\)
\({\rm{E}}F = \sqrt {{1^2} + {2^2} + {1^2}} = \sqrt 6 \)
$2. K$ là trung điểm của \({C_1}{D_1} \Rightarrow K\left( {1,2,2} \right)\)
\( \Rightarrow \overrightarrow {EK} = \left( {0,2,2} \right) \Rightarrow \left[ {\overrightarrow {EK} ,\overrightarrow {{\rm{E}}F} } \right] = \left( { - 2, - 2,2} \right)\)
Suy ra mặt phẳng $(EKF)$ có vectơ pháp tuyến là \(\left( { - 1, - 1,1} \right)\) và có phương trình: \( - x - y + z + 1 = 0\)
Khoảng cách từ $C$ đến mặt phẳng $(EKF)$ là \(\frac{{| - 2 - 2 + 0 + 1|}}{{\sqrt {{1^2} + {1^1} + {1^2}} }} = \sqrt 3 \)
Lại có \(\left[ {\overrightarrow {{\rm{EF}}} ,\overrightarrow {BD} } \right] = \left( {\left| {_2^2{\rm{ }}\left. {{}_2^2} \right|,\left| {_1^0{\rm{ }}\left. {{}_{ - 1}^{ - 2}} \right|,} \right.\left| {_{ - 1}^{ - 2}{\rm{ }}\left. {{}_2^2} \right|} \right.} \right.} \right) \Rightarrow \left| {\left[ {\overrightarrow {{\rm{EF}}} ,\overrightarrow {BD} } \right]} \right| = \sqrt {{2^2} + {2^2} + {2^2}} = \sqrt {12} \)
Gọi \(\varphi \)là góc giữa hai đường thẳng $EF$ và $BD$ thì \(c{\rm{os}}\varphi = \frac{{\left| {\overrightarrow {{\rm{EF}}} ,\overrightarrow {BD} } \right|}}{{\left| {\overrightarrow {{\rm{EF}}} } \right|.\left| {\overrightarrow {BD} } \right|}} = \frac{{\sqrt 3 }}{2} \Rightarrow \varphi = {30^0}\)
|
|
|
Đăng bài 26-04-12 03:45 PM
|
|