$1.$ Ta có mặt phẳng $(AA'D'D)//(BB'C'C)$ và $AD' \in (AA'D'D),B'C \in (BB'C'C)$ nên khoảng cách giữa hai đường thẳng chéo nhau $A'D$ và $B'C$ bằng khoẳng cách giữa hai mặt phẳng song song $(AA'D'D) va (BB'C'C)$ nghĩa là bằng $AB=a$ (Lưu ý có thể thấy rằng đườngvuông góc chung của $AD'$ và $B'C$ là đường nối các trung điểm của chúng)
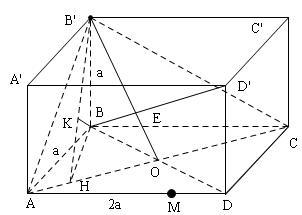
$2.$ Ta có $AC$ và $BD$ cắt nhau tại $O$ là trung điểm của mỗi đường, do đó
$d(D,(AB'C))=d(B,(AB"C))$
(kí hiệu $d(M,P)$ là khoảng cách từ $M$ đến mặt phẳng $(P))$.
Mặt khác vì $MA=\frac{3}{4}DA $ nên$ d(M,(AB'C))=\frac{3}{4} d(D,(AB'C))=\frac{3}{4} d(B,(AB'C))$
Kẻ $BH\bot AC,BK\bot B'H,$ta có$AC\bot(BB'H)$ nên $AC\bot BK\Rightarrow BK\bot (AB'C)$
do đó $d(M,(AB'C))=\frac{3}{4} BK (1)$
Trong tam giác vuông $ABC$ có
$\frac{1}{BH^2} =\frac{1}{BA^2}+\frac{1}{BC^2}=\frac{1}{a^2} +\frac{1}{4a^2}=\frac{5}{4a^2}$
Trong tam
giác vuông $BB’H$:
$\frac{1}{BK^2}=\frac{1}{BH^2}+\frac{1}{BB’^2}=\frac{5}{4a^2}+\frac{1}{a^2}=\frac{9}{4a^2}\Rightarrow
BK=\frac{2a}{3}$
Vậy $d(M,(AB'C))=\frac{3}{4} BK=\frac{3}{4}.\frac{2a}{a} =\frac{a}{2} $
$3.$ Tính thể tích tứ diện $AB'D'C$
Nối $BD'$ cắt $B'O$ tại $E$ ta có:
$\frac{D'E}{EB} =\frac{B'D'}{BO} =2$ (vì $B'D'//BO$)
$\Rightarrow d(D',(AB'C))=2d(B,(AB'C))$
$\Rightarrow V_{D'.AB'C}=2V_{B.AB'C}$ (hai hình chóp có chung đáy $AB'C$)
Ta có
$V_{B.AB'C}=\frac{1}{3} BB'.S_{ABC}=\frac{1}{6} BB'.BA.BC=\frac{1}{6} a.a.2a=\frac{a^3}{3} $ (đvdt)
ĐS : $V=\frac{2a^3}{3} $