a) Đường thẳng AB đi qua điểm A và có vecto chỉ phương →a=(1;3;−1)
Đường thẳng Δ đi qua điểm M0(5;0;−4) và có vecto chỉ phương →b=(2;1;−2)
Ta có: [→a,→b]=(−5;0;−5),→AM0=(3;−1;−3)
Suy ra [→a,→b].→AM0=0
Vậy hai đường thẳng AB và Δ đồng phẳng, Ngoài ra hai vecto →a,→b không cùng phương nên hai đường thẳng AB và Δ cắt nhau
Đường thẳng AB có phương trình tham số: {x=2+ty=1+3tz=−1−t(t∈R)
Gọi I là giao điểm của đường thẳng AB và Δ.
Tọa độ của I ứng với t là nghiệm đúng của phương trình
{(2+t)−2(1+3t)−5=0(2+t)+2(1+3t)+2(−1−t)+3=0⇔t=−1
Suy ra I(1;−2;0)
Ta có: →IA=(1;3;−1),→IB=(3;9;−3)⇒→IA,→IB cùng hướng. Vậy hai điểm A,B nằm cùng một phía đối với Δ
b) Phương tình của
(α) qua
A và vuông góc với
Δ:2(x−2)+1(y−1)−2(z+1)=0⇔2x+y−2z−7=0Gọi H là trung điểm của AC thì H là hình chiếu vuông góc của A trên đường thẳng Δ. Tọa độ của H là nghiệm đúng của hệ phương trình:
{x−2y−5=0x+2y−2z+3=02x+y−2z−7=0⇔{x=239y=−119z=−149⇒H(239;−119;−149)
⇒C(289;−329;−199)
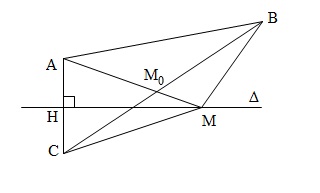
Do A và C là hai điểm đối xứng qua đường thẳng Δ nên với M là một điểm bất kì trên Δ ta có: MA=MC. Do đó: MA+MB=MC+MB≥BC
Đẳng thức xảy ra khi ba điểm B,C,M thẳng hàng. Khi đó M trùng với M0 là giao điểm của BC và đường thẳng Δ:
Đường thẳng BC có vecto chỉ phương →v=(4;47;−4)
phương trình tham số của đường thẳng BC:{x=4+4ty=7+47tz=−3−4t(t∈R)
Giao điểm M0 của Δ và BC ứng với t là nghiệm của hệ phương trình:
{(4+4t)−2(7+47t)−5=0(4+4t)+2(7+47t)+2(−3−4t)+3=0⇒t=−16
Suy ra M0(103;−56;−73)
Vậy max(MA+MB=BC)=√3223 khi M ở vị trí M0(103;−56;73)