|
|
Phép biến hình trong không gian: Phép biến hình $F$ trong không gian là 1 quy tắc để với 1 điểm $M$ trong không gian, xác định được 1 điểm $M'$ duy nhất gọi là ảnh của điểm $M$ qua Phép biến hình $F$ và ký hiệu $M' = F(M)$
Qua Phép biến hình $F$, mỗi hình (H) sẽ được biến thành hình (H’) gồm tất cả các ảnh của điểm thuộc hình (H)
1. Phép đối xứng qua mặt phẳng
Định nghĩa: Phép đối xứng qua mặt phẳng (P) là phép biến hình biến mỗi điểm thuộc (P) thành chính nó và biến mỗi điểm M không thuộc (P) thành điểm M’ sao cho (P) là mặt phẳng trung trực của đoạn MM’
Định lý 1: Nếu phép đối xứng qua mp(P) biến 2 điểm M, N lần lượt thành 2 điểm M’, N’ thì M’N’ = MN ( Phép đối xứng qua mặt phẳng là phép bảo toàn khoảng cách giữa 2 điểm bất kỳ )
2. Mặt phẳng đối xứng của 1 hình
Định nghĩa: Nếu phép đối xứng qua mặt phẳng (P) biến hình (H) thành chính nó thì (P) gọi là mặt phẳng đối xứng của hình (H)
Ví dụ :
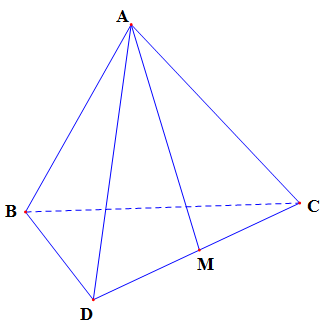
Cho tứ diện đều ABCD. Gọi M là trung điểm cạnh CD thì phép đối xứng qua mp(ABM) biến A thành B, B thành B, C thành D, D thành C. Như vậy phép đối xứng đó biến tứ diện ABCD thành chính nó, suy ra mp(ABM) là mặt phẳng đối xứng của tứ diện ABCD
Hình tứ diện đều ABCD có 6 mặt phẳng đối xứng, đó là mặt phẳng đi qua 1 cạnh và trung điểm cạnh đối diện
3. Hình bát diện đều và mặt phẳng đối xứng của nó
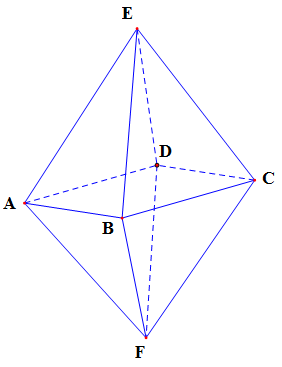
Hình vẽ là 1 hình đa diện có 8 mặt là những tam giác đều: EAB, EBC, ECD, EDA, FAB, FBC, FCD và FDA, có 6 đỉnh A, B, C, D, E, F; mỗi đỉnh là đỉnh chung cho 4 tam giác đều. Hình đó gọi là hình bát diện đều và ký hiệu là ABCDEF
Tính chất: 4 điểm A,B,C,D nằm trên 1 mặt phẳng và đó là mặt phẳng đối xứng của hình bát diện đều ABCDEF
4. Phép dời hình và sự bằng nhau của các hình
a) Định nghĩa phép dời hình: Một phép biến hình F trong không gian được gọi là 1 phép dời hình nếu nó bảo toàn khoảng cách giữa 2 điểm bất kỳ
- Phép đối xứng qua mặt phẳng là 1 phép dời hình. Phép đồng nhất ( biến mỗi điểm thành chính nó ) là 1 phép dời hình
- Hợp của những phép dời hình là phép dời hình
b) Một số ví dụ:
Ngoài phép đối xứng qua mặt phẳng, ta thường gặp 1 số phép dời hình sau:
- Phép tịnh tiến: phép tịnh tiến theo vecto $\overrightarrow {MM'} = \,\overrightarrow v $ là phép biến hình biến điểm M thành điểm M’ sao cho $\overrightarrow {MM'} = \,\overrightarrow v $
- Phép đối xứng qua đường thẳng ( phép đối xứng trục ): cho đường thẳng d, phép đối xứng qua đường thẳng d là phép biến hình biến mỗi điểm thuộc d thành chính nó và mỗi điểm M không thuộc d thành điểm M’ sao cho trong mặt phẳng (M,d), d là đường trung trực của đoạn MM’
- Phép đối xứng qua 1 điểm ( đối xứng tâm ): cho điểm O, phép đối xứng qua điểm O là phép dời hình biến mỗi điểm M thành điểm M’ sao cho $\overrightarrow {OM} + \overrightarrow {OM'} = \overrightarrow 0 $
c) Định nghĩa 2 hình bằng nhau: Hai hình (H) và (H’) được gọi là bằng nhau nếu có 1 phép dời hình biến hình này thành hình kia
Ví dụ:
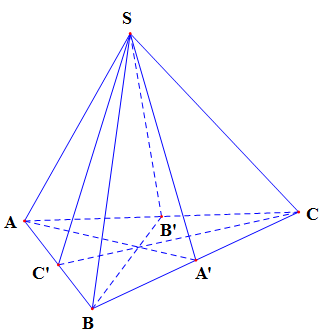
Cho hình chóp tam giác đều S.ABC. Gọi A’, B’, C’ lần lượt là trung điểm cạnh BC, CA, AB. Khi đó 2 tứ diện SABA’ và SBCB’ bằng nhau
Giải:
Thật vậy, phép đối xứng qua mp(SAA’) biến các điểm S,A,B,A’ lần lượt thành các điểm S,A,C,A’ và phép đối xứng qua mp(SCC’) biến các điểm S,A,C,A’ lần lượt thành các điểm S,B,C,B’. Như vậy qua 2 phép đối xứng trên, tứ diện SABA’ biến thành tứ diện SBCB’ nên 2 tứ diện đó bằng nhau
Định lý 2: Hai hình tứ diện ABCD và A’B’C’D’ bằng nhau nếu chúng có các cạnh tương ứng bằng nhau nghĩa là AB=A’B’, BC=B’C’, CD=C’D’, DA=D’A’, AC=A’C’, BD = B’D’
Hệ quả 1: Hai tứ diện đều có cạnh bằng nhau thì bằng nhau
Hệ quả 2: Hai hình lập phương có cạnh bằng nhau thì bằng nhau
|