Bài 106360

Question

Cho hình lập phương

$ABCD.A’B’C’D’$ cạnh

$a$ và một điểm

$M$ trên cạnh

$AB, AM = x, 0 < x < a$ . Xét mặt phẳng (

$P$ ) đi qua điểm

$M$ và chưa đường chéo

$A’C’$ của hình vuông

$A’B’C’D’.$

$1.$ Tính diện tích của thiết diện của hình lập phương cắt bởi mặt phẳng (

$P$ ).

$2.$ Mặt phẳng (

$P$ ) chia hình lập phương thành hai khối đã diện. Hãy tìm

$x$ để thể tích của một trong hai khối đa diện đó gấp đôi thể tích của khối đa diện kia.

score 0 · Answer 1

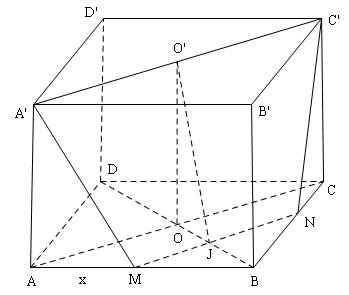
$1.$ Kẻ

$MN$ song song

$AC$ thì

$A’C’NM$ chính là thiết diện tạo thành.

$O’J$ là đường cao hình thang

$A’C’M’N’.$ (vì

$A'C'$ vuông góc với mp

$(OO'J)$ )

$\frac{OJ}{OB}=\frac{AM}{AB}\Leftrightarrow\frac{OJ}{\frac{a}{\sqrt{2}}}=\frac{x}{a}\Rightarrow{{OJ}} = \frac{{x\sqrt 2 }}{2} \Rightarrow O'J = \sqrt {{a^2} + \frac{{{x^2}}}{2}}$

$MN = MB.\sqrt 2 = (a - x)\sqrt 2$
Thiết diện có diện tích:

$S = \frac{1}{2}\left( {a\sqrt 2 + (a - x)\sqrt 2 } \right)\sqrt {{a^2} + \frac{{{x^2}}}{2}}$

$\Rightarrow S=\frac{1}{\sqrt{2}}(2a-x) \sqrt {{a^2} + \frac{{{x^2}}}{2}}$

$2. (P)$ chia hình lập phương thành

$2$ phần có thể tích gấp đôi nhau

$\Leftrightarrow A'C'NMB$ có thể tích

$= \frac{1}{3}$ thể tích hình lập phương

$= \frac{{{a^3}}}{3}$ . Ta có:

$\begin{array}{l} {V_{A'C'NBM}} = {V_{A'BMN}} + {V_{A'B'C'NB}}\\ = \frac{1}{6}{\left( {a - x} \right)^2}a + {V_{A'B'C'NB}} \end{array}$

$V_{A'B'C'NB}=V_{A'B'BN}+V_{A'B'C'N}=\frac{1}{6}a.a.(a-x)+\frac{1}{6}a.a^2$

$=\frac{a^2}{6}(2a-x)$
$\Rightarrow V_{A'C'NBM}=\frac{a}{6}(x^2-3ax+3a^2)$

YCBT

$\Leftrightarrow \frac{{{a^3}}}{3} = \frac{a}{6}\left( {{x^2} - 3ax + 3{a^2}} \right)$

$\Leftrightarrow x^2-3ax+a^2=0$

$\Leftrightarrow x = a\left( {\frac{{3 - \sqrt 5 }}{2}} \right)$

Bài 106360

1 Đáp án

Lý thuyết liên quan

Bài 106360

1 Đáp án

Liên quan

Sử dụng công thức thể tích tính khoảng cách

Lý thuyết liên quan