|
|
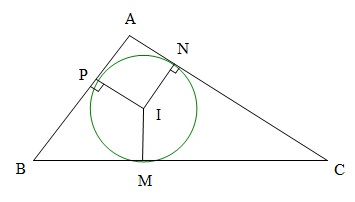
Ta có :
$\left\{ \begin{array}{l}
AP = AN = p - a\\
BM = BP = p - b\\
CN = CM = p - c
\end{array} \right.$ ($p$ là nửa chu vi $\Delta ABC$)
$\begin{array}{l}
\overrightarrow {IM} = \frac{{MC}}{{BC}}\overrightarrow {IB} + \frac{{MB}}{{BC}}\overrightarrow {IC} \\
\Rightarrow a\overrightarrow {IM} = \left( {p - c} \right)\overrightarrow {IB} + \left( {p - b} \right)\overrightarrow {IC} \,\,\,\,\,\,\,\,\,(1)
\end{array}$
Tương tự ,$\left\{ \begin{array}{l}
b\overrightarrow {IN} = \left( {p - a} \right)\overrightarrow {IC} + \left( {p - c} \right)\overrightarrow {IA} \,\,\,\,\,\,(2)\\
c\overrightarrow {IP} = \left( {p - b} \right)\overrightarrow {IA} + \left( {p - a} \right)\overrightarrow {IB} \,\,\,\,\,\,\,(3)
\end{array} \right.$
Cộng vế các đẳng thức $(1),(2),(3)$ thu được:
$\begin{array}{l}
a\overrightarrow {IM} + b\overrightarrow {IN} + c\overrightarrow {IP} = \left( {2p - b - c} \right)\overrightarrow {IA} + \left( {2p - a - c} \right)\overrightarrow {IB} + \left( {2p - a - b} \right)\overrightarrow {IC} \\
\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = a\overrightarrow {IA} + b\overrightarrow {IB} + c\overrightarrow {IC} \\
\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = \overrightarrow {0} \,\,\,\,\,\,
\end{array}$
Bài toán tổng quát: Với điểm J bất kỳ trong tam giác ABC, hạ $J{M_1},J{N_1},J{P_1}$ lần lượt vuông góc với $BC, CA, AB$.
Ta có : $\frac{a}{{J{M_1}}}\overrightarrow {J{M_1}} + \frac{b}{{J{N_1}}}\overrightarrow {I{N_1}} + \frac{c}{{J{P_1}}}\overrightarrow {J{P_1}} = \overrightarrow 0 $
|
|
|
Đăng bài 03-05-12 05:03 PM
|
|