|
|
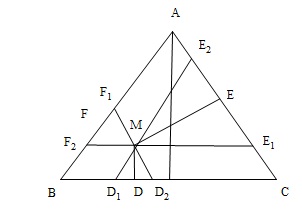
Cách $1$:
Qua $M$ kể các đường thẳng song song với các cạnh của tam giác $ABC$, chúng chia tam giác $ABC$ thành các tam giác đều ${M_1}{D_1}{D_2};M{E_1}{E_2};M{F_1}{F_2}$ và các hình bình hành $M{F_1}A{E_2};M{E_1}C{D_2};M{D_1}B{F_2}$
Ta có : $\left\{ \begin{array}{l}
\overrightarrow {MD} = \frac{1}{2}\left( {\overrightarrow {M{D_1}} + {{\overrightarrow {MD} }_2}} \right)\\
\overrightarrow {ME} = \frac{1}{2}\left( {\overrightarrow {M{E_1}} + \overrightarrow {M{E_2}} } \right)\\
\overrightarrow {MF} = \frac{1}{2}\left( {\overrightarrow {M{F_1}} + \overrightarrow {M{F_2}} } \right)
\end{array} \right.$
Cộng từng vế $3$ đẳng thức ta được
$\begin{array}{l}
\overrightarrow {MD} + \overrightarrow {ME} + \overrightarrow {MF} = \frac{1}{2}\left( {\overrightarrow {M{F_1}} + \overrightarrow {M{E_2}} } \right) + \frac{1}{2}\left( {\overrightarrow {M{D_1}} + \overrightarrow {M{F_2}} } \right) + \frac{1}{2}\left( {\overrightarrow {M{E_1}} + \overrightarrow {M{D_2}} } \right)\\
\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = \frac{1}{2}\left( {\overrightarrow {MA} + \overrightarrow {MB} + \overrightarrow {MC} } \right)\\
\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = \frac{1}{2}3\overrightarrow {MO} \\
\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = \frac{3}{2}\overrightarrow {MO\,} \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,(dpcm)
\end{array}$
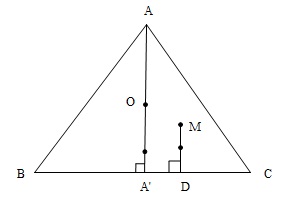
Cách $2$
Gọi $AA', BB', CC'$ là các đường cao của tam giác $ABC$.
Đặt : $S\left( {MBC} \right) = {S_a},S\left( {MCA} \right) = {S_b},S\left( {MAB} \right) = {S_c}$. ta có : ${S_a}\overrightarrow {MA} + {S_b}\overrightarrow {MB} + {S_c}\overrightarrow {MC} = \overrightarrow 0 \,\,\,\,\,\,\,(1)$
Mặt khác : $\overrightarrow {MD} = \frac{{MD}}{{{\rm{AA}}'}}.\overrightarrow {AA'} = \frac{{{S_a}}}{S}\overrightarrow {AA'} = \frac{3}{2}\frac{{{S_a}}}{S}\overrightarrow {AO} (S = S\left( {ABC} \right))$
Tương tự như vậy : $\overrightarrow {ME} = \frac{3}{2}.\frac{{{S_b}}}{S}\overrightarrow {BO} ;\,\,\,\,\overrightarrow {MF} = \frac{3}{2}.\frac{{{S_c}}}{S}\overrightarrow {CO} $
Từ đó suy ra : $\begin{array}{l}
\overrightarrow {MD} + \overrightarrow {ME} + \overrightarrow {MF} = \frac{3}{{2S}}\left( {{S_a}\overrightarrow {AO} + {S_b}\overrightarrow {BO} + {S_c}\overrightarrow {CO} } \right)\\
= \frac{3}{{2S}}.\left[ {{S_a}\left( {\overrightarrow {MO} - \overrightarrow {MA} } \right) + {S_b}\left( {\overrightarrow {MO} - \overrightarrow {MB} } \right) + {S_c}\left( {\overrightarrow {MO} - \overrightarrow {MC} } \right)} \right]\\
= \frac{3}{{2S}}\left( {{S_a} + {S_b} + {S_c}} \right)\overrightarrow {MO} - \frac{3}{{2S}}\left( {{S_a}\overrightarrow {MA} + {S_b}\overrightarrow {MB} + {S_c}\overrightarrow {MC} } \right)
\end{array}$
$ = \frac{3}{{2S}}.S.\overrightarrow {MO} $
$ = \frac{3}{2}\overrightarrow {MO} $ (đpcm)
Cách $1 $ biến đổi đơn giản và dễ nhớ hơn cách $2$.
|
|
|
Đăng bài 04-05-12 08:36 AM
|
|