|
|
$\frac{{{h_a}}}{{{l_a}}} = \frac{{AH}}{{AD}} = \cos \widehat {HAD}$
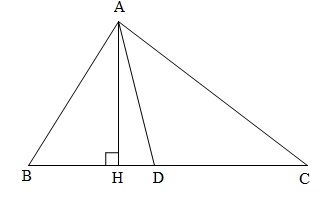
• Trường hợp $B \le {90^\circ}$
$\begin{array}{l}
\widehat {HAD} = \widehat {BAD} - \widehat {BAH}\\
\,\,\,\,\,\,\,\,\,\,\,\,\, = \frac{A}{2} - \left( {{{90}^\circ} - B} \right)\\
\,\,\,\,\,\,\,\,\,\,\,\, = \frac{A}{2} - \left( {\frac{{A + B + C}}{2} - B} \right)\\
\,\,\,\,\,\,\,\,\,\,\, = \frac{{B - C}}{2}
\end{array}$
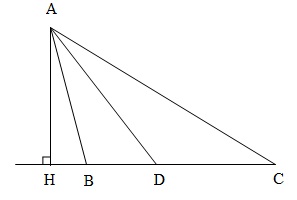
• Trường hợp $B > {90^\circ}$
$\begin{array}{l}
\widehat {HAD} = \widehat {BAD} + \widehat {BAH}\\
\,\,\,\,\,\,\,\,\,\,\,\, = \frac{A}{2} + \left( {B - {{90}^\circ}} \right)\\
\,\,\,\,\,\,\,\,\,\,\, = \frac{A}{2} + \left( {B - \frac{{A + B + C}}{2}} \right)\\
\,\,\,\,\,\,\,\,\,\,\, = \frac{{B - C}}{2}
\end{array}$
Tóm lại trong cả hai trường hợp đều có
$\widehat {HAD} = \frac{{B - C}}{2}$ .
Vậy $\frac{{{h_a}}}{{{l_a}}} = \cos\widehat {HAD} = \cos\frac{{B - C}}{2}$ (đpcm).
|
|
|
Đăng bài 04-05-12 05:45 PM
|
|