Bài 106705

Question

Cho elip:

$4x^2 + 16y^2 = 64$

$1.$ Xác định các tiêu điểm

$F_1; F_2$ , tâm sai và vẽ elip.

$2.$

$M$ là một điểm bất kì trên elip. Chứng tỏ rằng tỷ số khoảng cách từ

$M$ tới tiêu điểm phải

$F_2$ và tới đường thẳng

$x= \frac{8}{{\sqrt 3 }}$ có giá trị không đổi.

$3.$ Cho đường tròn (

$C$ ):

${x^2} + {y^2} + 4\sqrt 3 .x - 4 = 0$
Xét đường tròn (

$C’$ ) di động nhưng luôn luôn đi qua tiêu điểm phải

$F_2$ và tiếp xúc ngoài với đường tròn (

$C$ ). Chứng tỏ rằng các tâm

$N$ của đường tròn (

$C’$ ) nằm trên một Hypebol cố định. Viết phương trình của hypebol đó.

score 0 · Answer 1

$1.$ Phương trình elip có thể viết lại thành:

$\frac{{{x^2}}}{{{4^2}}} + \frac{{{y^2}}}{{{2^2}}} = 1$

$\Rightarrow a = 4,\,b = 2\,,\,\,c\, = \sqrt {12}$
Các tiêu điểm lần lượt là

${F_1}\left( { - \sqrt {12} ;0} \right)\,\,;\,\,{F_2}\left( {\sqrt {12} ;0} \right)$
Tâm sai của Elip là:

$e = \frac{c}{a} = \frac{{\sqrt 3 }}{2}$

$2.$

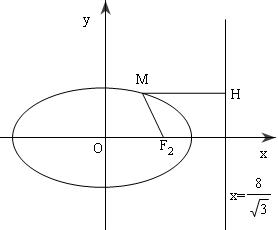
Xét điểm

$M(x_0;y_0)$ tùy ý đã cho thuộc Elip. Gọi

$H$ là hình chiếu vuông góc của

$M$ lên đường thẳng

$x = \frac{8}{{\sqrt 3 }}$ .
Ta có:

$M{F_2} = a - {\rm{e}}{{\rm{x}}_0} = \frac{{8 - \sqrt 3 {x_0}}}{2}$

$MH = \frac{8}{{\sqrt 3 }} - {x_0} = \frac{{8 - \sqrt 3 {x_0}}}{{\sqrt 3 }}$

$\Rightarrow \frac{{M{F_2}}}{{MH}} = \frac{{\sqrt 3 }}{2} \Rightarrow$ Tỉ số khoảng cách từ

$M$ tới tiêu điểm phải

$F_2$ và tới đường thẳng

$x = \frac{8}{{\sqrt 3 }}$ có giá trị không đổi.

$3.$

(

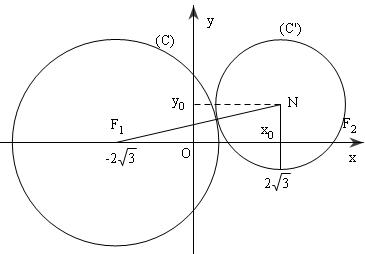
$C$ ) có phương trình:

$\begin{array}{l} {x^2} + {y^2} + 4\sqrt 3 x - 4 = 0\\ \Leftrightarrow {\left( {x + 2\sqrt 3 } \right)^2} + {y^2} = 16 \end{array}$
Do đó (

$C$ ) có tâm là

${F_1}( - 2\sqrt 3 ;0)\,\,\,\,;\,\,\,R = 4$
Gọi

$({x_0};{y_0})$ là tâm và

$r$ là bán kính của đường tròn (

$C’$ ) qua

$F_2$ và tiếp xúc (

$C$ ) thì (

$C’$ ) có phương trình:

${\left( {x - {x_0}} \right)^2} + {(y - {y_0})^2} = {r^2}$
Vì

${F_2}(\sqrt {12} ;0) \in (C') \Rightarrow {\left( {\sqrt {12} - {x_0}} \right)^2} + {\left( {0 - {y_0}} \right)^2} = {r^2}\,\,(1)$
Vì (

$C$ ) và (

$C’$ ) tiếp xúc ngoài nên:

$R + r = F_1N$

$\begin{array}{l} \Leftrightarrow 4 + r = {F_1}N\\ \Leftrightarrow {(4 + r)^2} = {\left( {{x_0} + 2\sqrt 3 } \right)^2} + y_0^2\\ \Leftrightarrow 16 + 8r + {r^2} = x_0^2 + 4\sqrt 3 {x_0} + 12 + y_0^2\,\,\,(2) \end{array}$
Thế (

$1$ ) vào (

$2$ ) ta có:

$r = \sqrt 3 {x_0} - 2$ , thế trở lại vào (

$1$ ) và rút gọn ta được:

$\begin{array}{l} 2x_0^2 - y_0^2 = 8\\ \Leftrightarrow \frac{{x_0^2}}{4} - \frac{{y_0^2}}{8} = 1 \end{array}$
Do đó tâm

$N({x_0};{y_0})$ của (

$C’$ ) luôn nằm trên một Hypebol cố định

$\frac{{x_0^2}}{4} - \frac{{y_0^2}}{8} = 1$

Bài 106705

1 Đáp án

Lý thuyết liên quan

Bài 106705

1 Đáp án

Liên quan

ĐƯỜNG HYPEBOL

Lý thuyết liên quan